set和multiset容器的操作函数和一道题：HDU 4989 Summary

一、开始

  1. 使用set或multiset之前，必须加入头文件
  2. set的含义是集合，它是一个有序的容器，里面的元素都是排序好的，支持插入，删除，查找等操作，就像一个集合一样。所有的操作的都是严格在logn时间之内完成，效率非常高。

  3. set 和multiset容器的内部结构通常由平衡二叉树(balancedbinary tree)来实现。当元素放入容器中时，会按照一定的排序法则自动排序，默认是按照less<>排序规则来排序。两者不同之处在于，multisets允许元素重复，而set不允许重复。
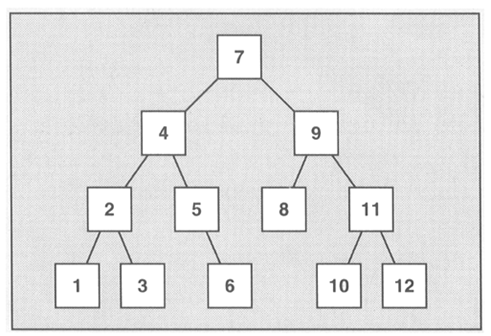
    平衡二叉树：
    </div>

  4. 这种自动排序的特性加速了元素查找的过程，但是也带来了一个问题：不可以直接修改set或multiset容器中的元素值，因为这样做就可能违反了元素自动排序的规则。如果你希望修改一个元素的值，必须先删除原有的元素，再插入新的元素。

  5. sets和multisets具有以下特点：
  • 不提供直接用来存取元素的任何操作元素
  • 通过迭代器进行元素的存取。

    二、set和multiset容器的操作函数

    1. 构造、拷贝、析构

Name Feature
set c 创建一个空的set或multiset容器
set c(op) 创建一个空的使用op作为排序法则的set或multiset容器
set c1(c2) 创建一个已存在的set或multiset容器的复制品，容器的类型和所有元素一同复制
set c(beg, end) 创建一个set或multiset容器，并且以[beg, end)范围中的元素进行初始化
set c(beg, end, op) 创建一个使用op作为排序法则的set或multiset容器，并且以[beg, end)范围中的元素进行初始化
c.~set() 容器的析构函数，销毁所有的元素，释放所有的分配内存

上面的set可以是下面几种形式：

Name Feature
set 以less<>为排序法则的set
set 以op为排序法则的set
multiset 以less<>为排序法则的multiset
multiset 以op为排序法则的multiset

2. 非变动性操作

Name Feature
c.size() 返回当前的元素数量
c.empty () 判断大小是否为零，等同于0 == size()，效率更高
c.max_size() 返回能容纳的元素最大数量
c1 == c2 判断c1是否等于c2
c1 != c2 判断c1是否不等于c2(等同于!(c1==c2))
c1 < c2 判断c1是否小于c2
c1 > c2 判断c1是否大于c2
c1 <= c2 判断c1是否小于等于c2(等同于!(c2<c1))
c1 >= c2 判断c1是否大于等于c2 (等同于!(c1<c2))

值得注意的是比较操作符只针对相同类型的容器，元素类型和排序法则类型都必须相同。
error例子如下：

1
2
3
4
5
std::set<float> c1;
std::set< float, std::greater<float> > c2;
...
if(c1 == c2) //error: different types
...

3. 特殊的搜寻函数

　sets和multisets在元素快速搜寻方面做了优化设计，提供了特殊的搜寻函数，所以应优先使用这些搜寻函数，可获得对数复杂度，而非STL的线性复杂度。比如在1000个元素搜寻，对数复杂度平均十次，而线性复杂度平均需要500次。

Name Feature
count (elem) 返回元素值为elem的个数
find(elem) 返回元素值为elem的第一个元素，如果没有返回end()
lower _bound(elem) 返回元素值为elem的第一个可安插位置，也就是元素值 >= elem的第一个元素位置
upper _bound (elem) 返回元素值为elem的最后一个可安插位置，也就是元素值 > elem 的第一个元素位置
equal_range (elem) 返回elem可安插的第一个位置和最后一个位置，也就是元素值==elem的区间

成员函数find()搜寻出与参数值相同的第一个元素，并返回一个迭代器，指向该位置。如果没有找到这样的元素，就返回容器的end()。
下面我们看一个lower_bound(), upper_bound和equal_range(val)例子，或者看博客介绍STL二分法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>
#include <set>
using namespace std;
int main()
{
    multiset<int> coll;

    coll.insert(1); //插入元素
    coll.insert(2);
    coll.insert(4);
    coll.insert(5);
    coll.insert(6);

    cout << "lower_bound(3):" << *coll.lower_bound(3) << endl;
    cout << "upper_bound(3):" << *coll.upper_bound(3) << endl;
    cout << "equal_range(3):" << *coll.equal_range(3).first
         << " " << *coll.equal_range(3).second << endl;

    cout << "lower_bound(5):" << *coll.lower_bound(5) << endl;
    cout << "upper_bound(5):" << *coll.upper_bound(5) << endl;
    cout << "equal_range(5):" << *coll.equal_range(3).first << " "
         << *coll.equal_range(3).second<< endl;
}
程序输出：
lower_bound(3):4
upper_bound(3):4
equal_range(3):4 4
lower_bound(5):5
upper_bound(5):6
equal_range(5):4 4

4. 赋值操作

set和multiset容器只提供最基本的赋值操作：

Name Feature
c1 = c2 把c2的所有元素复制到c1中，同时c1原有的元素被销毁。
c1.swap(c2) 交换c1和c2的元素。
swap(c1, c2) 同上，只不过这是一个通用算法。

需要注意的是两个容器的类型要一致（包括元素类型和排序法则类型）。

5. 迭代器函数

  • sets和multisets的迭代器是双向迭代器，对迭代器操作而言，所有的元素都被视为常数，可以确保你不会人为改变元素值，从而打乱既定顺序，所以无法调用变动性算法，如remove()。
  • set和multiset不提供元素直接存取，所以只能采用迭代器
Name Feature
c.begin() 返回一个随机存取迭代器，指向第一个元素
c.end() 返回一个随机存取迭代器，指向最后一个元素的下一个位置
c.rbegin() 返回一个逆向迭代器，指向逆向迭代的第一个元素
c.rend() 返回一个逆向迭代器，指向逆向迭代的最后一个元素的下一个位置

6. 安插和删除元素

Name Feature
c.insert(elem) 插入一个elem副本，返回新元素位置，无论插入成功与否。
c.insert(pos, elem) 安插一个elem元素副本，返回新元素位置，pos为收索起点，提升插入速度。
c.insert(beg,end) 将区间[beg,end)所有的元素安插到c，无返回值。
c.erase(elem) 删除与elem相等的所有元素，返回被移除的元素个数。
c.erase(pos) 移除迭代器pos所指位置元素，无返回值。
c.erase(beg,end) 移除区间[beg,end)所有元素，无返回值。
c.clear() 移除所有元素，将容器清空

删除：

1
2
3
4
5
6
7
auto to_delete = *it;
      auto tmp_it = chop_set.find(to_delete);
      while(tmp_it != chop_set.end()) {
          //note: erase will return next avilable it pointer
          it = chop_set.erase(tmp_it); 
          tmp_it = chop_set.find(*tmp_it);
      }

7. set实例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <set>
using namespace std;

int main()
{
    // empty set container
    set <int> gquiz1;

    gquiz1.insert(40);
    gquiz1.insert(30);
    gquiz1.insert(60);
    gquiz1.insert(20);
    gquiz1.insert(50);
    gquiz1.insert(50); // only one 50 will be added to the set
    gquiz1.insert(10);

    // printing set gquiz1
    cout << "\nThe set gquiz1 is : ";
    for(auto x : gquiz1)
        cout << x << "  ";
    cout << endl;

    // assigning the elements from gquiz1 to gquiz2
    set <int> gquiz2(gquiz1.begin(), gquiz1.end());
    // printing set gquiz1
    cout << "\nThe set gquiz2 is : ";
    for(auto x : gquiz2)
        cout << x << "  ";
    cout << endl;


    // remove all elements up to 30 in gquiz2
    cout << "\ngquiz2 after removal of elements less than 30 : ";
    gquiz2.erase(gquiz2.begin(), gquiz2.find(30));
    for(auto x : gquiz2)
        cout << x << "  ";
    cout << endl;

    // remove all elements with value 50 in gquiz2
    int num;
    num = gquiz2.erase (50);
    cout << "\ngquiz2.erase(50) : ";
    cout << num << " removed \t" ;
    for(auto x : gquiz2)
        cout << x << "  ";
    cout << endl;

    //lower bound and upper bound for set gquiz1
    cout << "gquiz1.lower_bound(40) : "
         << *gquiz1.lower_bound(40) << endl;
    cout << "gquiz1.upper_bound(40) : "
         << *gquiz1.upper_bound(40) << endl;

    //lower bound and upper bound for set gquiz2
    cout << "gquiz2.lower_bound(40) : "
         << *gquiz2.lower_bound(40) << endl;
    cout << "gquiz2.upper_bound(40) : "
         << *gquiz2.upper_bound(40) << endl;

    return 0;

}
程序输出：
The set gquiz1 is : 10  20  30  40  50  60

The set gquiz2 is : 10  20  30  40  50  60

gquiz2 after removal of elements less than 30 : 30  40  50  60

gquiz2.erase(50) : 1 removed 	30  40  60
gquiz1.lower_bound(40) : 40
gquiz1.upper_bound(40) : 50
gquiz2.lower_bound(40) : 40
gquiz2.upper_bound(40) : 60

三、一道习题

HDU 4989 Summary

Problem Description
Small W is playing a summary game. Firstly, He takes N numbers. Secondly he takes out every pair of them and add this two numbers, thus he can get N(N - 1)/2 new numbers. Thirdly he deletes the repeated number of the new numbers. Finally he gets the sum of the left numbers. Now small W want you to tell him what is the final sum.
Input
Multi test cases, every case occupies two lines, the first line contain n, then second line contain n numbers a1, a2, ……an separated by exact one space. Process to the end of file.
[Technical Specification]
2 <= n <= 100
-1000000000 <= ai <= 1000000000
Output
For each case, output the final sum.
Sample Input
4
1 2 3 4
2
5 5
Sample Output
25
10
Hint
Firstly small W takes any pair of 1 2 3 4 and add them, he will get 3 4 5 5 6 7. Then he deletes the repeated numbers, he will get 3 4 5 6 7, Finally he gets the sum=3+4+5+6+7=25
代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
#include <set>
#include <cstdio>
using namespace std;
typedef long long ll;

int main()
{
    ll sum = 0, arr[110];
    int n;
    set<int>s;
    while(~scanf("%d",&n))
    {
        s.clear();
        for(int i = 0; i < n; i++)
            cin >> arr[i];
        for(int j = 0;j < n; j++)
            for(int k = j + 1; k < n ;k++)
                s.insert(arr[k] + arr[j]);
        for(auto x : s)
            sum += x;
        cout << sum << endl;
        sum = 0;
    }
    return 0;
}