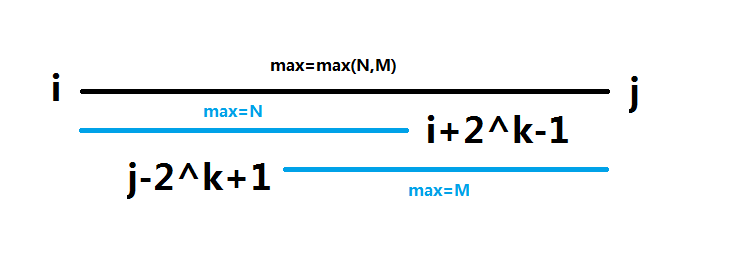区间最值查询

参考：https://blog.csdn.net/qq_41311604/article/details/79900893

RMQ

RMQ（Range Minimum/Maximum Query），即区间最值查询，这是一种在线算法，所谓在线算法，是指用户每次输入一个查询，便马上处理一个查询。RMQ算法一般用较长时间做预处理，时间复杂度为O(nlogn)，然后可以在O(1)的时间内处理每次查询。

求dp

现假设有一数组arr={1,3,6,7,4,2,5}；

设dp[i][j]表示从第i位开始连续2^j个数中的最小值。

例如dp[2][1]表示从第二位开始连续两个数的最小值（也就是从第二位数到第三位数的最小值），即3，6中的最小值，所以dp[2][1] = 3;

那么怎么求dp[2][1]呢？

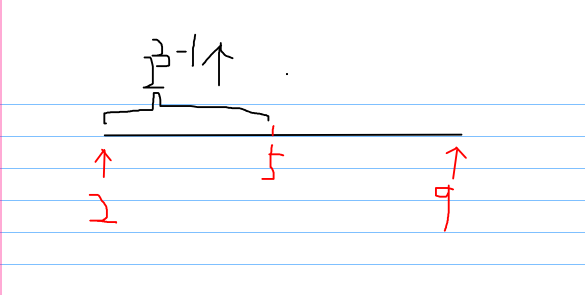
  1. 当i=2，j=3时，求dp[2][3]

    因为2^3=8，代表从2开始有8个数，所以范围为[2,9]
    然后我们可以将其按照类似二分的思想将其拆分为两部分
    所以中间mid=(2+9)/2=5

    • 左区间[2,5]：有4个数，其对应dp[2][2]
    • 右区间[6,9]：有4个数，其对应dp[6][2]

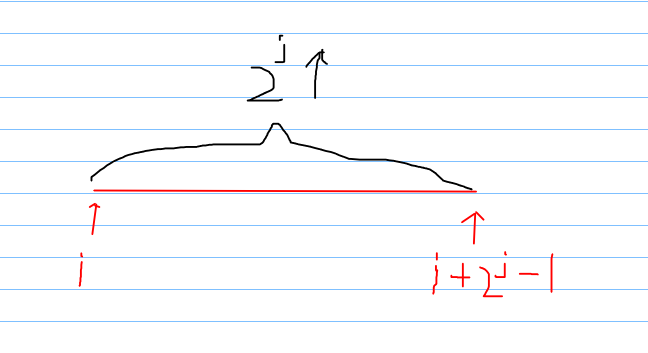
  2. 推广到普遍情况

    对照上面例子，因为平分，所以每个区间都可以分到一半的数(因为j是2的次方)，所以j肯定是j-1，2^(j-1)代表除以2^j/2，接着i就是很常见的位置关系了
    左区间：dp[i][j-1]
    右区间：dp[i+(2^j)/2][j-1]

所以

1
dp[i][j] = min(dp [i][j - 1], dp [i + (1 << j - 1)][j - 1])
1
2
3
4
5
6
7
8
9
10
11
/*
先更新每两个元素中的最小值，然后通过每两个元素的最小值获得每4个元素中的最小值，依次类推更新所有长度的最小值
*/
void rmq_init()
{
    for(int i = 1; i <=N; i++)
        dp[i][0] = arr[i];//初始化
    for(int j = 1; (1<<j) <= N; j++) //2^j不超过N
        for(int i = 1; i+(1<<j)-1 <= N; i++)
            dp[i][j]=min(dp[i][j-1], dp[i+(1<<j-1)][j-1]);
}

查询dp

得到了dp数组，那么怎么得到区间[l,r]最小值呢？我们只需要对每个二分区间进行取min就行了，首先我们得到这个区间是2的几次方

1
k = log2(r - l + 1);

然后2^k取到前面那些数的最小值，还没有覆盖整个区间，所以我们可以从后面再取最小值，最后再两者取最小就行了。

所以

1
RMQ[l,r] = min(dp[l][k], dp[r - (1 << k) + 1][k]);
1
2
3
4
5
int rmq(int l,int r)
{
    int k=log2(r-l+1);
    return min(dp[l][k],dp[r-(1<<k)+1][k]);
}

poj3264—Balanced Lineup

题意：有N头奶牛，按1-n编号，并给出他们的高度，有q次询问，求每次询问的一段编号区间内最高的牛和最矮的牛的身高差

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
/*
G++: 8172K	3579MS	 c++: 7964K	1813MS  
(微软的C++比开源的G++，快了将近一)
2019-04-26 19:40:00
*/
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

const int MAXN = 1E5;
int maxn[MAXN][20], minn[MAXN][20];
int n, q, num;

void RMQ()
{
    for(int j = 1; (1 << j) <= n; j++)
    {
        for(int i = 1; i+(1<<j)-1 <= n; i++)
        {
            minn[i][j]=min(minn[i][j-1], minn[i+(1<<j-1)][j-1]);
            maxn[i][j]=max(maxn[i][j-1], maxn[i+(1<<j-1)][j-1]);
        }
    }
}

int RMQ_MAX(int L, int R)
{
   //log2()报错的话可以用log的换底公式
    int k = log(double(R-L+1))/log(2.0);
    return max(maxn[L][k],maxn[R-(1<<k)+1][k]);
}

int RMQ_MIN(int L, int R)
{
    int k = log(double(R-L+1))/log(2.0);
    return min(minn[L][k],minn[R-(1<<k)+1][k]);
}

int main()
{
    scanf("%d %d", &n, &q);
    for(int i = 1; i <= n; i++)
    {
        scanf("%d", &num);
        maxn[i][0] = minn[i][0] = num;
    }
    RMQ();
    int L, R;
    while(q--)
    {
        scanf("%d %d", &L, &R);
        if(L > R)
            swap(L, R);
        printf("%d\n", RMQ_MAX(L, R) - RMQ_MIN(L, R));
    }
    return 0;
}