线段树入门

数据结构—线段树（segment tree）

引入

给定一个数组，数组长度可能非常大。现在我们需要对数组里面的数据反反复复进行两个操作

  • 求出某一个区间里面所有元素之和，(query操作)
  • 修改某个元素的值，(update操作)

暴力解决和前缀和

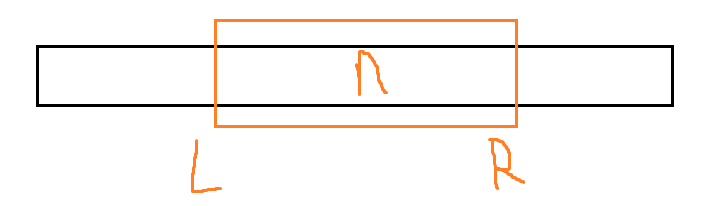
对区间[L,R]（长度为n）取和，并且更新一个元素i的值，采用暴力解决方法

可得

  • query(L,R)时间复杂度为O(n)
  • update(i)时间复杂度为O(1)

如果区间范围很大，再加上多次操作，暴力取和明显会超时，可以采用前缀和方式优化查询
sum_arr[0]=arr[0]
sum_arr[1]=arr[0]+arr[1]
sum_arr[2]=arr[0]+arr[1]+arr[2]

这样，假如我们想得到区间[2,4]的和，我们可以用sum_arr[4]-sum_arr[1]计算到

  • query(L,R)时间复杂度减小为O(1)
  • 因为改变一个值后，要同时更新后面的sum_arr数组，所以update(i)时间复杂度增大为O(n)

如果用线段树的话，我们可以将查询和更新的的时间复杂度都变为O(logn)

方法 query update
暴力 O(n) O(1)
前缀和 O(1) O(n)
线段树 O(logn) O(logn)

线段树简介

线段树是一种二叉搜索树，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logn)。是一种可以在很短的时间内对某个区间进行操作的数据结构。

可用于：
单点修改、区间修改、区间查询（如：区间求和，求区间最大值，求区间最小值……）

线段树构建

数组下标 1 2 3 4 5
数组元素 1 3 5 7 9

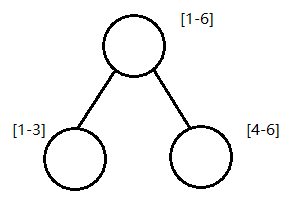
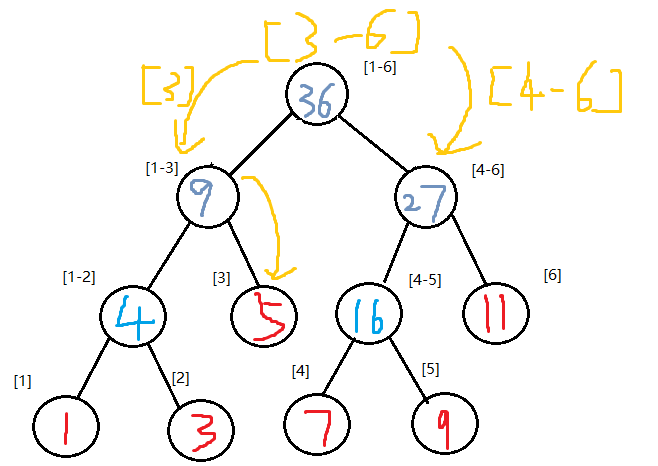
树根保存的是区间[1-6]中元素的和，其左孩子保存区间[1-3]所有元素的和，右孩子则是[4-6]

它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。
其划分区间方法类似于二分

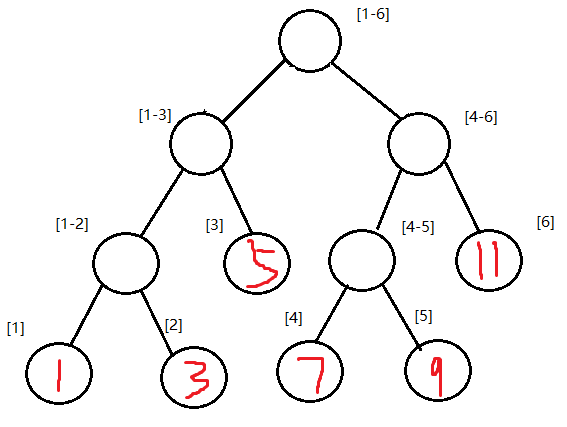
然后给每个叶子结点赋值

数组下标 1 2 3 4 5
数组元素 1 3 5 7 9

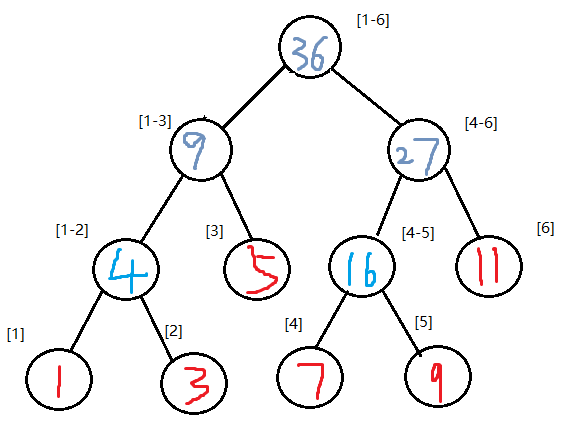
接着由孩子结点构成双亲结点

数组下标 1 2 3 4 5
数组元素 1 3 5 7 9

回到原题

如何找到[2-5]这个区间的和

根节点记录的是[1-6]的和，可以把[3-6]分成两半，左边找的是[3],右边是[4-6]，右边可以直接得到[4-6]的和为27，而[3]可以通过[1-3]得到和为5，最终结果为27+5=32。
这样子可以省掉很多搜索的时间，最坏情况是把整棵树都搜索一遍，时间复杂度为O(logn)

那么如何更新呢，假如我们想把第5个元素由9变成5

我们先找到9那个结点，然后把其值变为6，接着顺着一条路从下往上一直更新。
同样，更新的时间复杂度也是O(logn)

线段树的实现

由于线段树是用二叉树结构储存的，而且是近乎完全二叉树的，所以我使用了数组tree来存储
数组下标从1开始，同时添加虚结点使其变成完全二叉树

数组下标 1 2 3 4 5
数组元素 36 9 27 4 5

树的结点的定义

1
2
3
4
5
6
7
struct node
{
    int value; //节点对应区间的权值（不唯一，也可以代表区间最大值等）
    int left, right; //区间[left, right]
};
struct node tree[1000];
int father[100]; //记录某个点的序号，方便查找对应的数组下标

建树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Build_tree(1, 1, 6);
//为区间[left, right]建立一个以top为祖先的线段树，top为根节点下标
void Build_tree(int top, int left, int right)
{
    tree[top].left = left; //写入第index个结点的左区间
    tree[top].right = right; //写入第index个结点的右区间
    tree[top].value = 0; //每个区间的值初始化为0

    if(left == right)	//区间长度为0时，赋值并且结束递归
    {
    	tree[top].value = arr[left];
        father[left] = top;
        return;
    }
    int mid = (right + left) / 2; //取区间中点
    int left_node = top * 2; //左孩子下标
    int right_node = top * 2 + 1;  //右孩子下标
    Build_tree(left_node, left, mid);  //往左孩子方向继续建立线段树
    Build_tree(right_node, mid + 1, right);  //往右孩子方向继续建立线段树
    //更新结点值为左右孩子的和
    tree[top].value = tree[left_node].value + tree[right_node].value; 
}

更新

更新数组的第5个元素的值为6，直接在树里面更新该结点的值后，然后从父结点往上更新，直到更新到了根结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main()
{
    tree[father[5]].value = 6;
    Update(father[5]);
}

void Update(int index)	//index为要修改那个点的数组下标
{
    int father_node = index / 2; //父结点下标
    int left_node = father_node * 2;   //左孩子下标
    int right_node = father_node * 2 + 1;   //右孩子下标
    tree[father_node].value = tree[left_node].value + tree[right_node].value; //更新值
    if(father_node == 1) //找到树的根结点，终止退出
    	return;
    Update(father_node); //递归更新，由父结点往上找
}

查询[L,R]区间


先查询左子树：

  1. 如果满足条件3 >= L,则要查询的区间有涉及左子树，例如查询[1,2]，[2,4]
    • 如果满足3 >= R,则要查询的区间完全在左子树，例如[1,2]，这时候要查询的区间不变
    • 如果不满足3 >= R,则要查询的区间不完全在左子树，例如[2,4]，这时候就需要查询在左子树那边的区间，所以要查询[2,3]

90%
同理再查询右子树：

  1. 如果满足条件R >= 4,则要查询的区间有涉及右子树，例如查询[4,6]，[2,5]
    • 如果满足L >= 4,则要查询的区间完全在右子树，例如[4,6]，这时候要查询的区间不变
    • 如果不满足L >= 4,则要查询的区间不完全在右子树，例如[2,5]，这时候就需要查询在右子树那边的区间，所以要查询[4,5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//从index开始查询，所以index一般为树的根结点,查询的区间是[L,R]，结果保留在ans里面
void Query(int index, int L, int R, int& ans){
    if(tree[index].left == L && tree[index].right == R){ //找到了一个完全重合的区间
        ans += tree[index].value;
        return;
    }
    int left_node = index*2;
    if(L <= tree[left_node].right){ //左区间有涉及
    	if(R <= tree[left_node].right) //全包含于左区间，查询区间不变
        	Query(left_node, L, R, ans);
        else //半包含于左区间，则查询区间拆分，左端点不变，右端点变为左孩子的右区间端点
        	Query(left_node, L, tree[left_node].right, ans);
    }
    int right_node = left_node + 1;
    if(R >= tree[right_node].left){ //右区间有涉及
    	if(L >= tree[right_node].left) //全包含于右区间，查询区间不变
        	Query(right_node, L, R, ans);
        else //半包含于左区间，则查询区间拆分，与上同理
        	Query(right_node, tree[right_node].left, R, ans);
    }
}

模板题HDU1754

936MS 8336K（注意，线段树需要空间比较大，数组开小可能会wa或者TLE，一般为4n）

线段树部分优化

  1. a*2可以用a<<1代替，a/2可以用a>>1代替。（位运算其实就是直接对在内存中的二进制数据进行操作，因此处理数据的速度非常快）
  2. 因为下标为a的节点的左儿子下标为a*2，右儿子下标为a*2+1，所以可以
1
2
3
4
5
//加入一些编译预处理指令可以提高编程效率，加快编译速度
#define LS(a) (a << 1)
// a<<1 等同于 a*2
#define RS(a) (a << 1 | 1)
// a<<1|1 等同于 a*2+1

线段树进阶

  1. Lazy标记—用于同时更新一段区间的值：poj3468 A Simple Problem with Integers
  2. 线段树离散化（节约空间）—poj2528 Mayor’s posters
  3. 线段树应用：扫描线问题（求多个矩形互相覆盖后的面积）：poj1151 Atlantis
  4. 可持久化（保留整个操作的历史）—主席树