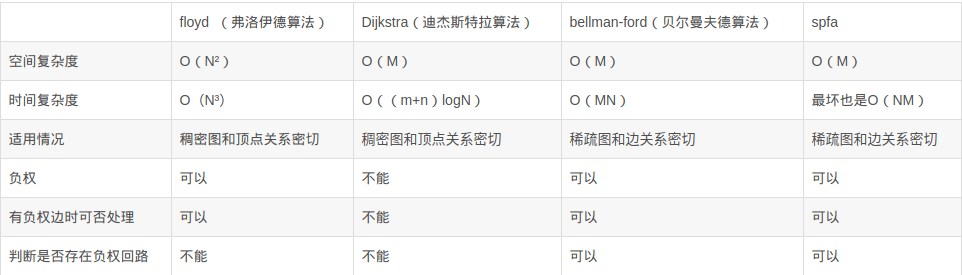
Floyd,Dijkstra, Spfa
(E为边个数,V为顶点个数)

其中N表示点数,M表示边数
Floyd 算法虽然总体上时间复杂度较高,但可以处理带负权边的图(但不能有负权回路),并且均摊到每一点对上,在所有的算法中还是属于比较优秀的算法。另外,floyd算法较小的编码复杂度也是一大优势,所以,如果要求的是所有点对间的最短路径,或者如果数据范围较小,则floyd算法比较合适。
Dijkstra算法最大的弊端就是他无法处理带有负权边以及负权回路的图,但是Dijkstra算法具有良好的可扩展性,扩展后可以适应很多问题。另外用堆优化的Dijkstra算法的时间复杂度可以达到O(M log N)。当边有负权,甚至存在负权回路时,需要使用Bellman-ford 算法或者队列优化的Bellman-ford算法,因此我们选择最短路径法时,根据实际的需求和每一种算法的特性,选择合适的算法来使用。
参考:https://blog.csdn.net/yuewenyao/article/details/81023035
Floyd(多源最短路)
Floyd算法用于求每一对顶点之间的最短路径,3个for循环就可以。时间复杂度O(v^3) 。v为图顶点个数
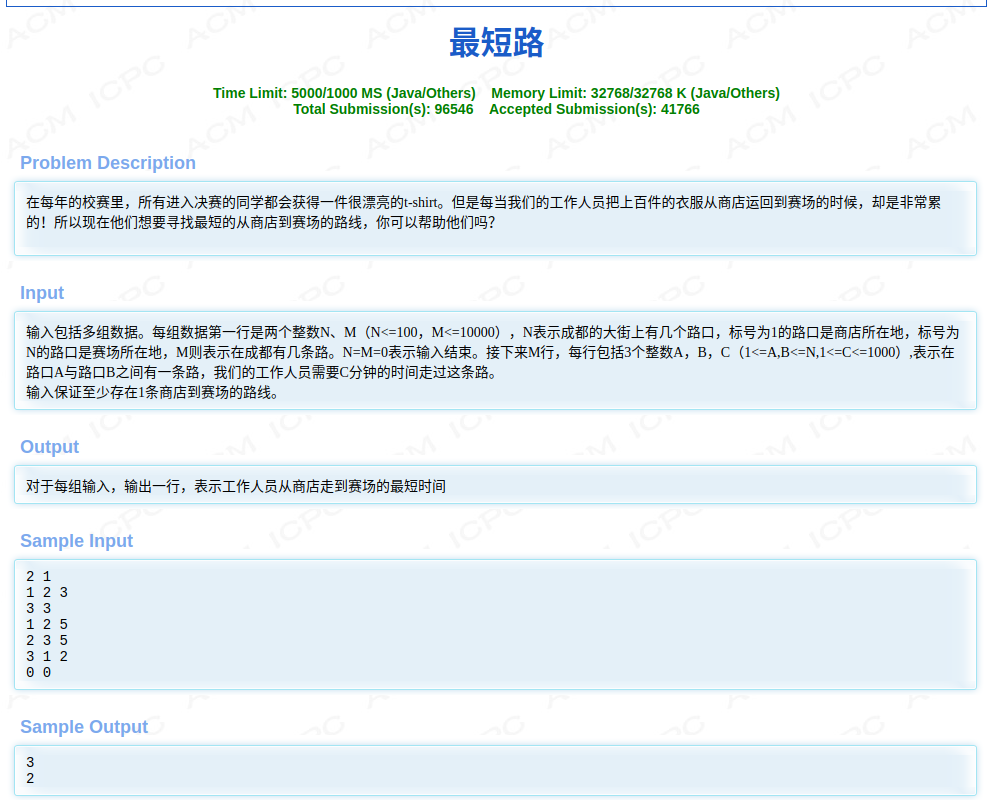
模板题:HDU2544-最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e2 + 10;
const int INF = 0X3F3F3F3F;
int dp[MAXN][MAXN];
int n, m, e1, e2, v;
void floyd()
{
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(cin >> n >> m && n && m)
{
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= i; j++)
{
if(i == j)
dp[i][j] = 0;
else
dp[i][j] = dp[j][i] = INF;
}
}
for(int i = 1; i <= m; i++)
{
cin >> e1 >> e2 >> v;
dp[e1][e2] = dp[e2][e1] = v;
}
floyd();
cout << dp[1][n] << endl;
}
return 0;
}
|
Dijkstra(单源最短路)
不采用最小优先队列,时间复杂度是O(v^2),v为图顶点个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
|
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 1e2 + 10;
const int INF = 0X3F3F3F3F;
int dp[MAXN][MAXN];
int vis[MAXN];
int dis[MAXN];
int n, m, e1, e2, v, MIN;
void dijkstra(int beg)
{
for(int i = 1; i <= n; i++)
{
vis[i] = 0;
dis[i] = dp[beg][i];
}
vis[beg] = 1;
for(int i = 1; i <= n; i++)
{
int k = 0;
MIN = INF;
for(int j = 1; j <= n; j++)
{
if(vis[j] == 0 && MIN > dis[j])
{
MIN = dis[j];
k = j;
}
}
vis[k] = 1;
for(int j = 1; j <= n; j++)
{
if(vis[j] == 0 && dis[k] + dp[k][j] < dis[j])
dis[j] = dis[k] + dp[k][j];
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(cin >> n >> m && n && m)
{
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= i; j++)
{
if(i == j)
dp[i][j] = 0;
else
dp[i][j] = dp[j][i] = INF;
}
}
for(int i = 1; i <= m; i++)
{
cin >> e1 >> e2 >> v;
dp[e1][e2] = dp[e2][e1] = v;
}
dijkstra(1);
cout << dis[n] << endl;
}
return 0;
}
|
Spfa
邻接表,队列优化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
|
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int MAXN = 10000 + 10;
const int INF = 0X3F3F3F3F;
struct node
{
int to, next, cost;
}edge[MAXN];
int head[MAXN];
int dis[MAXN];
int vis[MAXN];
int n, m, e1, e2, v, len;
void add(int from, int to, int cost)
{
edge[len].to = to;
edge[len].cost = cost;
edge[len].next = head[from];
head[from] = len++;
}
void spfa(int beg)
{
dis[beg] = 0;
vis[beg] = 1;
queue<int>q;
q.push(beg);
while(!q.empty())
{
int u = q.front();
q.pop();
vis[u] = 0;
for(int i = head[u]; i != -1; i = edge[i].next)
{
int v = edge[i].to;
int c = edge[i].cost;
if(dis[v] > dis[u] + c)
{
dis[v] = dis[u] + c;
if(vis[v] == 0)
{
vis[v] = 1;
q.push(v);
}
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
while(cin >> n >> m && n && m)
{
memset(head, -1, sizeof(head));
memset(vis, 0 , sizeof(vis));
memset(dis, INF, sizeof(dis));
len = 0;
for(int i = 1; i <= m; i++)
{
cin >> e1 >> e2 >> v;
add(e1, e2, v);
add(e2, e1, v);
}
spfa(1);
if(dis[n] == INF)
cout << "-1" << endl;
else
cout << dis[n] << endl;
}
return 0;
}
|