prim算法,kruskal算法,POJ1251入门题目
参考:https://blog.csdn.net/qq_40306845/article/details/81540626
模板题目
poj1251—Jungle Roads
题意:给你n个点,右n-1条边,每个边都有一个权值,让你求出最小生成树
题目说明不含重复边
prime
- 先任意选择一条边(一般直接选择第一条),连接与其相连权值最小的点,然后两个点成为一个集合体。
- 找这个不在这个集合体里 但是与集合体相连的权值最小的点 与集合体相连,并把该点归入集合体。
- 重复上一条操作,直到集合体归入了所有的点
时间复杂度
记顶点数v,边数e
邻接矩阵:O(v2) 邻接表:O(elog2v)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include <iostream>
#include <cstring>
using namespace std;
const int MAXN = 1e2;
int mp[MAXN][MAXN];
int vis[MAXN], ans[MAXN];
const int INF = 0x3f3f3f3f;
int n;
void prime()
{
int sum = 0;
for(int i = 1; i <= n; i++)
{
vis[i] = 0;
ans[i] = mp[1][i];
}
vis[1] = 1;
for(int i = 1; i <= n; i++)
{
int MIN = INF, pos = 0;
for(int j = 1; j <= n; j++)
{
if(!vis[j] && ans[j] < MIN)
{
MIN = ans[j];
pos = j;
}
}
if(MIN == INF)
break;
vis[pos] = 1;
sum += MIN;
for(int k = 1; k <= n; k++)
{
if(!vis[k] && mp[pos][k] < ans[k])
ans[k] = mp[pos][k];
}
}
cout << sum << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int m, k;
char c1, c2;
while(cin >> n && n)
{
memset(mp, INF, sizeof(mp));
for(int i = 1; i < n; i++)
{
cin >> c1 >> m;
while(m--)
{
cin >> c2 >> k;
mp[c1-'A'+1][c2-'A'+1] = mp[c2-'A'+1][c1-'A'+1] = k;
}
}
prime();
}
return 0;
}
|
kruskal
- 先选择一条权值最小的边,把这条边相连的两个点归成一个集合。
- 再找下一个权值最小的边,但是边相连的两个点不能属于同一个集合,把这条边相连的两个点(这里也可以是集合)归成一个集合
- 重复上一条操作,直到最后只有一个集合体且归入所有的点。
时间复杂度
elog2e (e为图中的边数)
prime与kruskal区别:
- 集合的个数:
prime算法自始自终只有一个集合,而kruskal算法可以有多个集合,所以kruskal算法要用到并查集。
- 选取的方式:
prime算法先是任意选取,再根据选取已有的基础上选取权值最小且不在集合的点(取点)。kruskal算法则是每次以权值最小的边来选取,可以有多个集合(取边)。
- 稠密图用prim比kcuskal快的不止一下,稀疏图kruskal更快。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| #include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 1e2;
int vis[MAXN];
struct node
{
int a,b;
int val;
}mp[MAXN*MAXN];
bool cmp(node x, node y)
{
return x.val < y.val;
}
int findFather(int x)
{
if(vis[x] == 0)
return x;
else
return vis[x] = findFather(vis[x]);
}
int n, len;
void kruskal()
{
int ans = 0, cnt = 0;
memset(vis, 0 ,sizeof(vis));
sort(mp, mp + len, cmp);
for(int i = 0; i < len; i++)
{
int x = findFather(mp[i].a);
int y = findFather(mp[i].b);
if(x != y)
{
vis[x] = y;
ans += mp[i].val;
cnt++;
if(cnt == n - 1)
break;
}
}
if(cnt != n - 1)
cout << "-1" << endl;
else
cout << ans << endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int m, k;
char c1, c2;
while(cin >> n && n)
{
len = 0;
for(int i = 1; i < n; i++)
{
cin >> c1 >> m;
while(m--)
{
cin >> c2 >> k;
mp[len].a = c1-'A'+1;
mp[len].b = c2-'A'+1;
mp[len].val = k;
len++;
}
}
kruskal();
}
return 0;
}
|

参考:
POJ 1751 Highways【最小生成树+输出路径】 - mengxiang000000 - CSDN博客
题意:给你n个村庄的坐标x,y,建立高速公路,并且已经给你了m条已经建好公路的村庄,让你输出还要建立的公路,并且输出该公路的两端的村庄编号,输出可以任意顺序;
此题就是求最小生成树+路径输出就行了,但是我们要处理已经联通了的村庄。怎么处理呢?
我们假设不相连的节点的权值为无穷大,
如果我们直接把两个已经联通的点的值更新为无穷大的话,明显不行

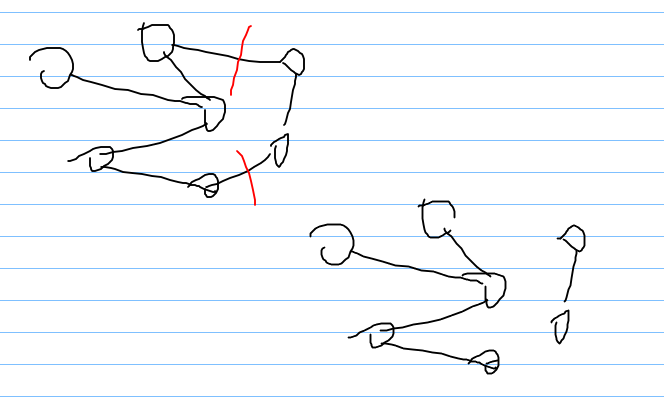
如上图,红色部分即已经联通了,如果我们直接把这2条路径更新为无穷大,就会变为不联通的情况,详细可看去掉红色部分的图。
我们可以将红色部分的值变为0,然后如果判断到了权值为0,那么就不用输出路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
|
#include <iostream>
#include <cstring>
using namespace std;
const int MAXN = 1e3;
int mp[MAXN][MAXN];
int vis[MAXN], ans[MAXN];
int path[MAXN];
struct node
{
int x,y;
}p[MAXN];
const int INF = 0x3f3f3f3f;
int n;
double Dist(node a,node b)
{
return (1.0*(a.x-b.x)*(a.x-b.x)+1.0*(a.y-b.y)*(a.y-b.y));
}
void prime()
{
for(int i = 1; i <= n; i++)
{
path[i] = 1;
vis[i] = 0;
ans[i] = mp[1][i];
}
vis[1] = 1;
for(int i = 1; i <= n; i++)
{
int MIN = INF, pos = 0;
for(int j = 1; j <= n; j++)
{
if(!vis[j] && ans[j] < MIN)
{
MIN = ans[j];
pos = j;
}
}
if(MIN != INF && MIN != 0)
cout << path[pos] << " " << pos << endl;
if(MIN == INF)
break;
vis[pos] = 1;
for(int k = 1; k <= n; k++)
{
if(!vis[k] && mp[pos][k] < ans[k])
{
ans[k] = mp[pos][k];
path[k] = pos;
}
}
}
}
int main()
{
memset(mp, INF, sizeof(mp));
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%d%d", &p[i].x, &p[i].y);
for(int j = 1; j < i; j++)
{
mp[i][j] = mp[j][i] = Dist(p[i], p[j]);
}
}
int m;
scanf("%d", &m);
int a, b;
while(m--)
{
scanf("%d%d", &a, &b);
mp[a][b] = mp[b][a] = 0;
}
prime();
return 0;
}
|