动态规划

入门

DP入门参考：漫画：什么是动态规划？

进阶参考：【DP专辑】ACM动态规划总结

http://www.cnblogs.com/raichen/p/5772056.html

动态规划原理

1-最优子结构

用动态规划求解最优化问题的第一步就是刻画最优解的结构，如果一个问题的解结构包含其子问题的最优解，就称此问题具有最优子结构性质。因此，某个问题是否适合应用动态规划算法，它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时，用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。

2-重叠子问题

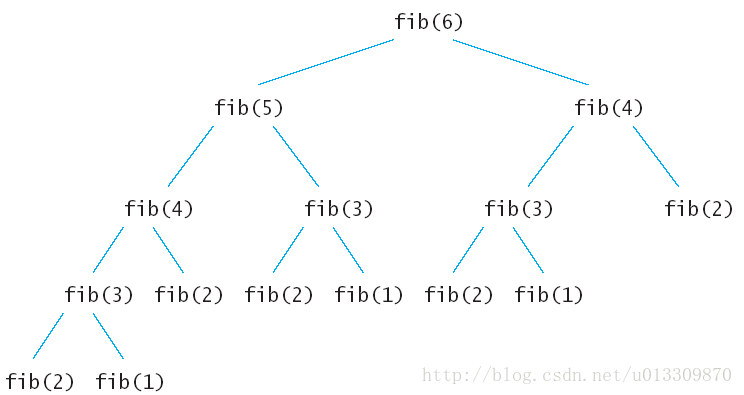
在斐波拉契数列，可以看到大量的重叠子问题，比如说在求fib（6）的时候，fib（2）被调用了5次。如果使用递归算法的时候会反复的求解相同的子问题，不停的调用函数，而不是生成新的子问题。如果递归算法反复求解相同的子问题，就称为具有重叠子问题（overlapping subproblems）性质。在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。

3-无后效性

将各阶段按照一定的次序排列好之后，对于某个给定的阶段状态，它以前各阶段的状态无法直接影响它未来的决策，而只能通过当前的这个状态。换句话说，每个状态都是过去历史的一个完整总结。这就是无后向性，又称为无后效性。

数塔系列

首先什么是“数塔类型”？从某一点转向另一点或者说是从某一状态转向另一状态，有多种选择方式（比如这里的9->12 , 9->15），从中选取一条能产生最优值的路径。

参考：

动态规划“数塔”类型题目总结

经典数塔HDU[2048]

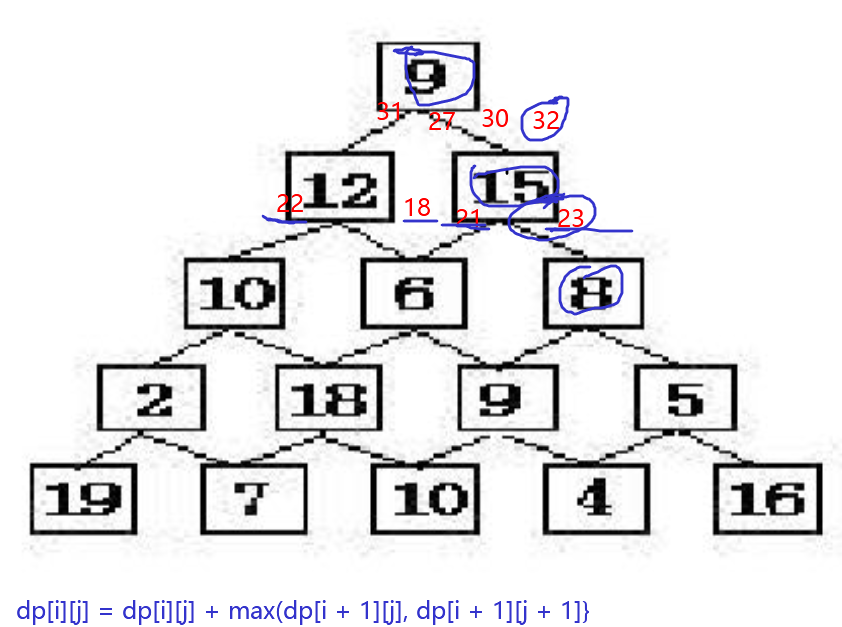
数塔问题 ：要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

数塔问题的经典解法是从后面算到前面，如果从前面算到后面很麻烦，因为后面一层有很多个数字是由少到多，如果反过来由多到少就简单了

分析：站在位置9，我们可以选择沿12方向移动，也可以选择沿着15方向移动，现在我们假设“已经求的”沿12方向的最大值x和沿15方向的最大值y，那么站在9的最大值必然是：Max(x,y) + 9。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-13 13:05:10
 Exe.Time:171MS	 Exe.Memory：1848k
*/

#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 111;
int Map[MAXN][MAXN];

int main()
{
    ios::sync_with_stdio(false);
    int test;
    cin >> test;
    while(test--)
    {
        int n;
        cin >> n;
        for(int i = 1; i <= n; i++)
            for(int j = 1; j <= i; j++)
                cin >> Map[i][j];
        for(int i = n - 1; i >= 1; i--)
        {
            for (int j = 1; j <= i; j++)
            {
                Map[i][j] = Map[i][j] + max(Map[i + 1][j], Map[i + 1][j + 1]);
            }
        }
        cout << Map[1][1] << endl;
    }
    return 0;
}

HDU1176[免费馅饼]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
第0秒                       5                         （这里的数字指的是第N秒可能到达的位置坐标）

第1秒                     4 5 6

第2秒                   3 4 5 6 7

第3秒                 2 3 4 5 6 7 8

第4秒               1 2 3 4 5 6 7 8 9

第5秒             0 1 2 3 4 5 6 7 8 9 10

第6秒             0 1 2 3 4 5 6 7 8 9 10

第7秒 .................  

可以发现从第5秒开始之后就都是 0 1 2 3 4 5 6 7 8 9 10

和“数塔”一样，它也是从某一点出发，有多个选择的问题（往前走一步，呆在原地，往后走一步）从中选择一条最优值路径（获得馅饼最多）。还是按照“数塔”的思考方式，我们可以假设“已经求得”下一个站在位置4获得的最大值x和呆在原地获得的最大值y以及站在位置6获得的最大值z,那么对于起始位置5获得最大值就是Max(x,y,z) ，因此可以得到状态转移方程为:

1
dp[t][x] += max(max(dp[t + 1][x - 1], dp[t + 1][x + 1]),dp[t + 1][x]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-13 17:53:03	
 Exe.Time:265MS	 Exe.Memory：10012k
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAXN = 110000;
int dp[MAXN][20];

int main()
{
    int n, Max, t, x;
    while(cin >> n && n)
    {
        Max = 0;
        memset(dp, 0, sizeof(dp));
        while(n--)
        {
            cin >> x >> t;
            if(t > Max) //记录最大时间，时间是纵坐标，落地点是横坐标
                Max = t;
            dp[t][x]++;
        }
        for(t = Max - 1; t >= 0; t--)
        {
            dp[t][0] += max(dp[t+1][0],dp[t+1][1]);//每行的第一个只有二种选择
            for(x = 1; x < 10; x++)
            {
                dp[t][x] += max( max(dp[t + 1][x - 1],dp[t + 1][x]),
                                    dp[t + 1][x + 1]);
            }
            dp[t][10] += max(dp[t + 1][9], dp[t + 1][10]); //每行的最后一个只有二种选择
        }
        cout << dp[0][5] << endl;//不是dp[1][5]，刚开始吃的不一定在5，有可能在4,6
    }
    return 0;
}

poj1088(滑雪)

1
2
3
4
5
6
依然和“数塔”一样，从某一点出发，面临多个选择（往上，往左，往下，往右）从中选择一条最优值路径（滑雪距离最长）
若对A点求，很显然它的最大值就为： Max(上，右，下，左) + 1
因此对于任意位置[i,j], 其状态转移方程为：m[i][j] = Max(m[i-1][j] , m[i][j+1] , m[i+1][j] , m[i][j-1]) + 1
由于这道题很难画出它的路径图（起点和终点都不知道）因此很难用“列表格”的方式自底向上求解。

解题思路：设一与输入数组对应的状态数组 dp，其值代表输入数组中此点的最长滑雪路径。使用广搜填表，最后遍历输出最大值即可    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-13 23:04:42	
 Exe.Time:79MS	 Exe.Memory：320k
*/

#include <iostream>
#include <cstring>
using namespace std;
int row, col; //二维数组的行与列

const int MAX = 1e2 + 10;
int Map[MAX][MAX];
int dp[MAX][MAX]; // 记录每一个点的最大滑雪长度

int check(int i, int j)
{
    return (i >= 1 && j >= 1 && i <= row && j <= col);
}

int BFS(int i, int j)
{
    int Max = 0;

    //判断右边能不能走，同时要满足右边的数小
    if(check(i, j + 1) && Map[i][j] > Map[i][j + 1])
    {
        if(dp[i][j + 1]) //如果之前走过，那就比较下是现在的线路的值还是之前的大
           Max = Max > dp[i][j + 1] ? Max : dp[i][j + 1];
        else //没有走过的话，那就需要BFS一遍
        {
            Max = Max > BFS(i, j + 1) ? Max : BFS(i, j + 1);
        }
    }

    // 向下广搜
    if (check(i + 1, j) && Map[i][j] > Map[i + 1][j])
    {
        if (dp[i + 1][j])
        {
            Max = Max > dp[i + 1][j] ? Max : dp[i + 1][j];
        }
        else
        {
            Max = Max > BFS(i + 1, j) ? Max : BFS(i + 1, j);
        }
    }

    // 向左广搜
    if (check(i, j - 1) && Map[i][j] > Map[i][j - 1])
    {
        if (dp[i][j - 1])
        {
            Max = Max > dp[i][j - 1] ? Max : dp[i][j - 1];
        }
        else
        {
            Max = Max > BFS(i, j - 1) ? Max : BFS(i, j - 1);
        }
    }

    // 向上广搜
    if (check(i - 1, j) && Map[i][j] > Map[i - 1][j])
    {
        if (dp[i - 1][j])
        {
            Max = Max > dp[i - 1][j] ? Max : dp[i - 1][j];
        }
        else
        {
            Max = Max > BFS(i - 1, j) ? Max : BFS(i - 1, j);
        }
    }

    // 如上下左右均不通，该点路径值为 1；
    // 否则取最大路径值加 1
    //将结果记录在dp数组中(记忆化搜索的重点)
    if (Max == 0)
        dp[i][j] = 1;
    else
        dp[i][j] = 1 + Max;

    return dp[i][j];

}
int main()
{
    ios::sync_with_stdio(false);
    while (cin >> row >> col)
    {
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= row; i++)
            for(int j = 1; j <= col; j++)
                cin >> Map[i][j];

        int ans = 0;
        for(int i = 1; i <= row; i++)
            for(int j = 1; j <= col; j++)
            {
                int tmp = BFS(i, j);
                if(tmp > ans)
                    ans = tmp;
            }
        cout << ans << endl;
    }
    return 0;
}

数位DP

数位dp是一种计数用的dp，一般就是要统计一个区间内满足一些条件数的个数。

参考：

数位dp总结 之 从入门到模板

数位dp记录——bili

HDU3555( Bomb )模板题

题目大意：在[0,n]的范围内存在多少个数字含有49

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/*
Judge Status : Accepted		Language : C++  
Submit Time：2018-08-07 15:54:05	
Exe.Time:93MS	 Exe.Memory：1796k
*/
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
int digit[20]; //存位数，最长20位
ll dp[20][2]; //dp[i][j]表示当前第i位，前一位的数字是否是j

//len:第len个数位，if_num:判断某一位是否到到达约束数位, limit:上一位是否有限制
ll dfs(ll len, bool if_num, bool limit)
{
    //递归边界，既然是按位枚举，最低位是0，那么len == 0说明这个数我枚举完了
    if(len == 0)
        return 1;
    //两个约束条件,limit防止前面的dp[len][if_num]让条件为真，比如dp[1][1]时，当百位有限制，
    // 而dp[1][1]之前有值了，如果没有limit，就会多算了。
    if(!limit && dp[len][if_num]) //不用去统计49
        return dp[len][if_num];
    ll cnt = 0, up = (limit ? digit[len] : 9); //up:如果到了限制那个数位，那么就限制，否则循环0-9
    for(int i = 0; i <= up; i++)
    {
        if(if_num && i == 9)
            continue;
        cnt += dfs(len - 1, i == 4, limit && i == up);
    }
    if(!limit) //如果没有约束，说明是完整计算的，那么就记忆下，下次直接就可以返回值了
        dp[len][if_num] = cnt;
    return cnt;
}

ll solve(ll num)
{
    int k = 0;
    while(num) //得到位数，存到k里面
    {
        digit[++k] = num % 10;
        num /= 10;
    }
    return dfs(k, false, true); //从最高位开始枚举
}

int main()
{
    ios::sync_with_stdio(false);
    ll n;
    cin >> n;
    while(n--)
    {
        memset(dp, 0, sizeof(dp));
        ll num;
        cin >> num;
        //solve:算的是没有49的个数
        cout << num + 1 - solve(num) << endl;
    }
    return 0;
}

稍微修改HDU2089(不要62)

在HDU3555基础上面多了一个区间，开始的时候是给出最大值m，区间是1～m，现在是区间是n～m，那么只要solve(m) - solve(n - 1)就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-07 18:22:21	
 Exe.Time:15MS	 Exe.Memory：1792k
*/
///标有改的注释是说这里相当于3555那道题变了
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;

int digit[20];
ll dp[20][2];

ll dfs(ll len, bool if_num, bool limit)
{
    if(len == 0)
        return 1;
    if(!limit && dp[len][if_num]) 
        return dp[len][if_num];
    ll cnt = 0, up = (limit ? digit[len] : 9); 
    for(int i = 0; i <= up; i++)
    {
        if(if_num && i == 2) //改
            continue;
        if(if_num ==4 || i == 4) //改
            continue;
        cnt += dfs(len - 1, i == 6, limit && i == up); //改
    }
    if(!limit) 
        dp[len][if_num] = cnt;
    return cnt;
}

ll solve(ll num)
{
    int k = 0;
    while(num) 
    {
        digit[++k] = num % 10;
        num /= 10;
    }
    return dfs(k, false, true); 
}

int main()
{
    ios::sync_with_stdio(false);
    ll n, m;
    while(cin >> n >> m && n && m)
    {
        memset(dp, 0, sizeof(dp));
        cout << solve(m) - solve(n - 1) << endl; //改
    }
    return 0;
}

牛客—区间内数字含有6的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*
 * Submit Time 2019-01-27 23:21:50
 */
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
 
int digit[20];
ll dp[20][2];
 
ll dfs(ll len, bool if_num, bool limit)
{
    if(len == 0)
        return if_num;
    if(!limit && dp[len][if_num])
        return dp[len][if_num];
    ll cnt = 0, up = (limit ? digit[len] : 9);
    for(int i = 0; i <= up; i++)
        cnt += dfs(len - 1, if_num || i == 6, limit &&i == digit[len]);
    if(!limit)
        dp[len][if_num] = cnt;
    return cnt;
}
 
ll solve(ll num)
{
    int k = 0;
    while(num)
    {
        digit[++k] = num % 10;
        num /= 10;
    }
    return dfs(k, false, true);
}
 
int main()
{
    ios::sync_with_stdio(false);
    ll n, m;
    while(cin >> n >> m)
    {
        memset(dp, 0, sizeof(dp));
        cout << solve(m) - solve(n - 1) << endl;
    }
    return 0;
}

LCIS—最长上升公共子序列

讲解：

zoj2432 hdoj1423 最长公共上升子序列（LCIS）

LCIS 最长公共上升子序列问题DP算法及优化

模板题HDU1423(Greatest Common Increasing Subsequence)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-09-07 21:30:12	
 Exe.Time:15MS	 Exe.Memory：5712KB
*/
#include <iostream>
using namespace std;
const int MAXN = 1E3;
int s1[MAXN], s2[MAXN];
int len1, len2;

int LCIS()
{
    int ans = 0;
    int dp[MAXN][MAXN]  = {0};
    for(int i = 0; i < len1; i++)
    {
        int maxdp = 0;
        for(int j = 0; j < len2; j++)
        {
            if(s1[i] != s2[j])
                dp[i + 1][j] = dp[i][j];
            if(s1[i] > s2[j] && maxdp < dp[i + 1][j])
                maxdp = dp[i + 1][j];
            if(s1[i] == s2[j])
                dp[i + 1][j] = maxdp + 1;
            if(dp[i + 1][j] > ans)
                ans = dp[i + 1][j];
        }

    }
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    int test;
    cin >> test;
    while(test--)
    {
        cin >> len1;
        for(int i = 0; i < len1; i++)
            cin >> s1[i];
        cin >> len2;
        for(int i = 0; i < len2; i++)
            cin >> s2[i];
        cout << LCIS() << endl;
        if(test)
            cout << endl;
    }
    return 0;
}

LIS—最长递增子序列

问题描述：找出一个n个数的序列的最长单调递增子序列： 比如A = {5,6,7,1,2,8} 的LIS是5,6,7,8

O(n^2)的复杂度

最优子结构

假设LIS[i] 是以arr[i]为末尾的LIS序列的长度。则：

LIS[i] = {1+Max(LIS(j))}; j<i, arr[j]<arr[i];

LIS[i] = 1, j<i, 但是不存在arr[j]<arr[i];

所以问题转化为计算Max(LIS(j)) 0<i<n

重叠的子问题

以arr[i] (1<= i <= n)每个元素结尾的LIS序列的值是 重叠的子问题。

所以填表时候就是建立一个数组DP[i], 记录以arr[i]为序列末尾的LIS长度。

DP[i]怎么计算？

遍历所有j<i的元素，检查是否DP[j]+1>DP[i] && arr[j]<arry[i] 若是，则可以更新DP[i]

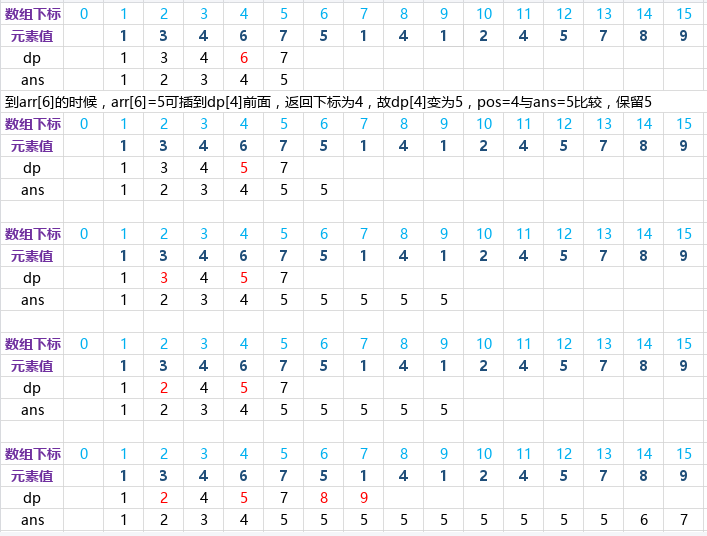
图示

  • arr[1]到arr[9]存值
  • LIS代表此元素到arr[1]的LIS
  • LIS来源代表是从哪个继承而来，值为数组下标

HDU1257(最少拦截系统)模板题

http://acm.hdu.edu.cn/showproblem.php?pid=1257

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-03 11:16:58	
 Exe.Time:62MS	 Exe.Memory：1844k
*/
#include <iostream>
#include <cstring>
using namespace std;

int LIS(int arr[], int len)
{
    const int dp_len = len + 10;

    int *dp = new int[dp_len];
    memset(dp, 0, sizeof(dp[0]) * dp_len); //创建动态数组并且初始化

   // int * dp = new int[dp_len]();

    arr[0] = -1e9;
    for(int i = 1; i <= len; i++)
        for(int j = 0; j < i; j++)
        {
            if(arr[i] > arr[j] && dp[i] < dp[j] + 1)
                dp[i] = dp[j] + 1;
        }

    int MAX = 0;
    for(int i = 1; i <= len; i++)  //找出dp数组中最大的那个值
    {
        if(dp[i] > MAX)
            MAX = dp[i];
    }

    delete[] dp;
    return MAX;
}

int main()
{
    ios::sync_with_stdio(false);
    int n;
    while(cin >> n)
    {
        int *arr = new int[n + 10];
        for(int i = 1; i <= n; i++)
            cin >> arr[i];
        cout << LIS(arr, n) << endl;
    }
    return 0;
}

参考：

算法设计 - LCS 最长公共子序列&&最长公共子串 &&LIS 最长递增子序列

【算法知识总结】最长递增子序列

【算法设计指南】最长递增子序列(微博/微信公众号:@算法时空—bilibili)

nlgn的复杂度

参考：

HRBU ACM 01背包 LIS 拓扑 凸包—-bilibili——20:41

这个比较难讲，看视频比较好理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-03 14:27:55	
 Exe.Time:15MS	 Exe.Memory：1884k
*/
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

int LIS(int arr[], int len)
{
    int *dp = new int[len + 10]();
    int ans = 0;
    for(int i = 1; i <= len; i++)
    {
        int pos = lower_bound(dp + 1, dp + ans + 1, arr[i]) - dp; 
        //求最长非递减序列可以将lower_bound变为upper_bound
        dp[pos] = arr[i];
        ans = max(ans, pos);
    }
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    int n;
    while(cin >> n)
    {
        int *arr = new int[n + 10]();
        for(int i = 1; i <= n; i++)
            cin >> arr[i];
        cout << LIS(arr, n) << endl;
    }
    return 0;
}

图示

LIS变形—有升有降

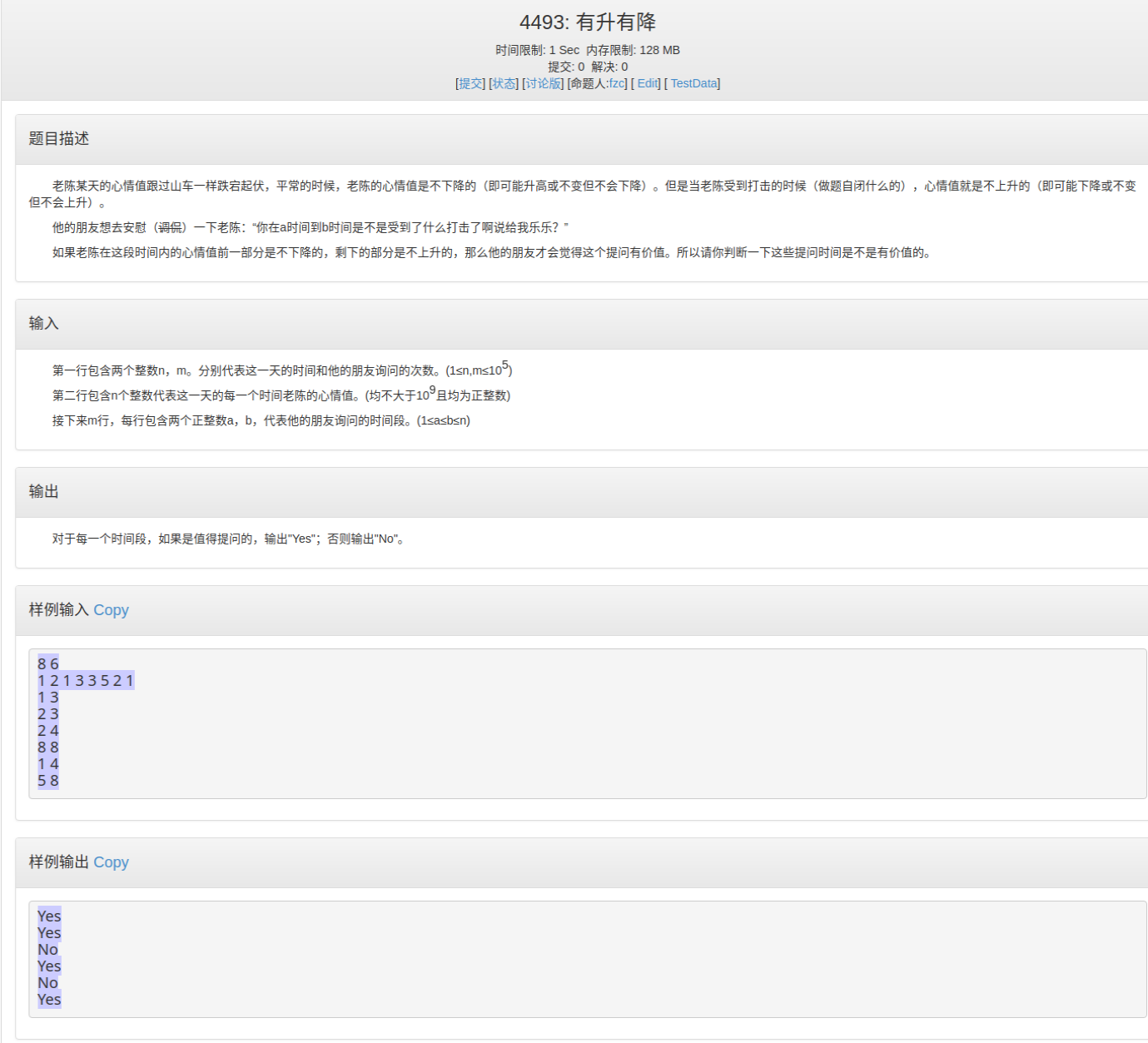
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
	Time:54 ms
    Memory:2252 kb
    2019-04-08 16:45:30
*/
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
const int MAXN = 1E5+10;
int arr[MAXN], dp[MAXN] = {0}, rdp[MAXN] = {0};
int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d", &arr[i]);
    for(int i = 1; i <= n; i++)
    {
        if(arr[i-1] >= arr[i])
            dp[i] = dp[i-1] + 1;
        else
            dp[i] = 1;
    }
     
    for(int i = n; i >= 1; i--)
    {
        if(arr[i+1] >= arr[i])
            rdp[i] = rdp[i+1] + 1;
        else
            rdp[i] = 1;
    }
     
    int n1, n2;
    while(m--)
    {
        scanf("%d %d", &n1, &n2);
        if(dp[n2] + rdp[n1] >= n2-n1+1)
            printf("Yes\n");
        else
            printf("No\n");
    }
    return 0;
}

最大递增子数组和

这个是由LIS O(n2)的办法变化而来的，因为O(nlgn)的那个代码的dp数组虽然保存的是一个最长递增序列，但是里面是最小的，不是最大的，所以只能由n2那个办法转变而来

这个动态规划可以先看前三项

  • dp[1] = num[1]

  • num[2]如果大于num[1]

    • dp[2] = dp[1] + num[2]

    • 否则dp[2] = num[2]

  • num[3]如果大于num[2]
    • 那么dp[3] = dp[2] + num[3]
  • 如果num[3]大于num[1]
    • dp[3] = dp[1] + num[3]
  • 如果num[3]不大于num[2]同时也不大于num[1]
    • dp[3] = num[3]。

说了这么多其实就是一个意思，用之前的每一个数和当前的数比较，比当前数小的就加上dp【之前数】，不然就等于当前数

参考:动态规划：HDU1087-Super Jumping! Jumping! Jumping!（最大上升子序列和）

HDU1087(Super Jumping! Jumping! Jumping!)模板题

http://acm.hdu.edu.cn/showproblem.php?pid=1087

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-03 18:38:13
 Exe.Time:31MS	 Exe.Memory：1828k
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

int LIS(int arr[], int len)
{
    const int dp_len = len + 10;
    int * dp = new int[dp_len]();

    arr[0] = -1e9;
    int MAX = -1e9;
    for(int i = 1; i <= len; i++)
    {
        for(int j = 0; j <= i; j++)
        {
            if(arr[i] > arr[j]) //之前数比当前数小，就加上当前数到之前数的和上面
                dp[i] = max(dp[i], dp[j] + arr[i]);
        }
        dp[i] = max(dp[i], arr[i]);	//之前数都不比当前数小的情况下直接就是当前数
        if(dp[i] > MAX)	//记录最大的那个和
            MAX = dp[i];
    }
    delete[] dp;
    return MAX;
}

int main()
{
    ios::sync_with_stdio(false);
    int n;
    while(cin >> n && n)
    {
        int *arr = new int[n + 10]();
        for(int i = 1; i <= n; i++)
            cin >> arr[i];
        cout << LIS(arr, n) << endl;
    }
    
    return 0;
}

LCS—最长公共子序列

找两个字符串的最长公共子串，这个子串要求在原字符串中是连续的。而最长公共子序列则并不要求连续。

cnblogs与belong，最长公共子序列为blog（cnblogs, belong），最长公共子串为lo（cnblogs, belong）这两个问题都是用空间换空间，创建一个二维数组来记录之前的每个状态

解释参考：LCS（最长公共子序列）注意：是可以不连续的，区别于最长公共子串

poj1458（Common Subsequence）模板题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-09 11:45:50	
 Exe.Time:0MS	 Exe.Memory：1036k
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXDP = 1e3;
const int MAXS = 1e7;
int dp[MAXDP][MAXDP];
char s1[MAXS], s2[MAXS];

int LCS(char* s1, char* s2)
{
    int len1 = strlen(s1) - 1;//因为s1,s2是从1开始存的，所以长度要减1
    int len2 = strlen(s2) - 1;
    for(int i = 0; i <= len1; i++)
        for(int j = 0; j <= len2; j++)
        {
            if(i == 0 || j == 0)
                dp[i][j] = 0;
            else if(s1[i] == s2[j])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
        /*
        for(int i = 0; i <= len1 ; i++)
        {
            for(int j = 0;j <= len2; j++)
                cout << dp[i][j] << " ";
            cout << endl;
        }
        */

        return dp[len1][len2];
}
int main()
{
    s1[0] = ' ', s2[0] = ' ';
    ios::sync_with_stdio(false);
    while(cin >> s1 +1 >> s2 + 1)
        cout << LCS(s1, s2) << endl;
    return 0;
}

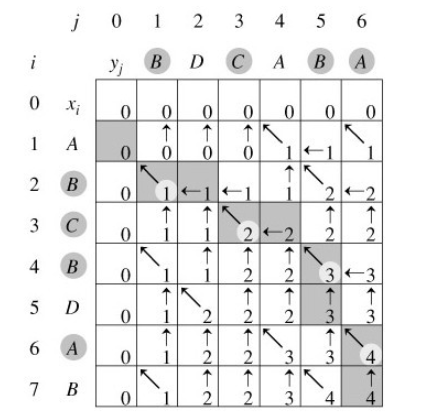
HDU1503(Advanced Fruits)还原最长公共子序列、记录路径

1
可以用pre[i][j]来记录dp[i][j]状态转移时是从哪种状态转移过来的，一共就三种：dp[i−1][j−1]+1,dp[i−1][j],dp[i][j−1]。然后从dp[len0][len1]开始往前递归，遇到从dp[i−1][j−1]+1状态转移的情况就标记，直到递归到dp[0][]或者dp[][0]结束。

参考：https://blog.csdn.net/Ramay7/article/details/52003368

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-10 11:33:40		
 Exe.Time:62MS	 Exe.Memory：9620k
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXDP = 1e3;
const int MAXS = 1e7;

int dp[MAXDP][MAXDP];
char s1[MAXS], s2[MAXS];
int pre[MAXDP][MAXDP]; //dfs需要，记录状态
int vis[MAXDP];  //记录第一个串中哪些位置被用掉
int len_s1, len_s2; //s1,s2的长度

void dfs(int len1, int len2)
{
    if(len1 == 0 || len2 == 0)
        return;
    if(pre[len1][len2] == 1)
    {
        vis[len1] = 1;
        dfs(len1 - 1, len2 - 1);
    }
    else if(pre[len1][len2] == 2)
        dfs(len1, len2 - 1);
    else
        dfs(len1 - 1, len2);
}

void LCS(char* s1, char* s2)
{
    len_s1 = strlen(s1) - 1;
    len_s2 = strlen(s2) - 1;
    for(int i = 0; i <= len_s1; i++)
        for(int j = 0; j <= len_s2; j++)
        {
            if(i == 0 || j == 0)
                dp[i][j] = 0;
            else if(s1[i] == s2[j])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
                pre[i][j] = 1;
            }
            else
            {
                if(dp[i][j - 1] > dp[i - 1][j])
                {
                    dp[i][j] = dp[i][j - 1];
                    pre[i][j] = 2;
                }
                else
                {
                    dp[i][j] = dp[i - 1][j];
                    pre[i][j] = 3;
                }
            }
        }
}

void print()
{
    int st = 1;
    for(int i = 1; i <= len_s1; ++i)
    {
        if(vis[i] == 1)
        {
            for(int j = st; j <= len_s2; ++j)
            {
                if(s1[i] == s2[j])
                {
                    st = j + 1;
                    break;
                }
                cout << s2[j];
            }
        }
        cout << s1[i];
    }
    for(int j = st; j <= len_s2; ++j)
        cout << s2[j];
    cout << endl;
}

int main()
{
    s1[0] = ' ', s2[0] = ' ';
    ios::sync_with_stdio(false);
    while(cin >> s1 +1 >> s2 + 1)
    {
        memset(dp, 0, sizeof(dp));
        memset(pre, 0, sizeof(pre));
        memset(vis, 0, sizeof(vis));
        LCS(s1, s2);
        dfs(len_s1, len_s2);
        print();
    }
    return 0;
}

poj1080(Human Gene Functions)LCS应用

题意

给定两个基因字符串，用A，C，G，T表示其组成成分。若两个基因的长度不一样，可以通过在两个串中分别添加空格使其长度一致。当其长度一样后，分别计算对应位置上的两个字母的分数，并将所有的分数相加便得到两个串的相似度分数。求，两个基因串的最高分数。

1
设dp(i,j)为第一个序列(s1)的前i个数和第二个序列(s2)的前j个数的相似度的最大值。当s1[i-1]==s2[j-1]时，由题目给出的表显然可以得出dp(i,j)=dp(i-1,j-1)+score[s1[i-1]][s2[j-1]];score数组为题目中给出的那个表格。当s1[i-1]!=s2[j-1]时，由普通的LCS显然有dp(i,j)=max(d(i-1,j)+score[s1[i-1]]['-'],dp(i,j-1)+score['-'][],d(i-1,j-1)+score[s1[i-1]][s2[j-1]])。于是，两个for就解决问题了。注意初始化数组。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-07-29 12:43:57	
 Exe.Time:0MS	 Exe.Memory：0.6MB
*/
#include <iostream>
#include <algorithm>
using namespace std;

const int LEN = 1e3;
int dp[LEN][LEN];
int score[LEN][LEN];
char c1[LEN];
char c2[LEN];
int len1, len2;

void init()
{
    score['A']['A']=score['C']['C']=score['G']['G']=score['T']['T']=5;
    score['A']['C']=score['C']['A']=score['A']['T']=score['T']['A']=score['T'][' ']=score[' ']['T']=-1;
    score['A']['G']=score['G']['A']=score['C']['T']=score['T']['C']=score['G']['T']=score['T']['G']=score['G'][' ']=score[' ']['G']=-2;
    score['A'][' ']=score[' ']['A']=score['G']['C']=score['C']['G']=-3;
    score['C'][' ']=score[' ']['C']=-4;

    dp[0][0] = 0;
    for(int i = 0; i < len1; i++)
        dp[0][i + 1] = dp[0][i] + score[c1[i]][' '];
    for(int i = 0; i < len2; i++)
        dp[i + 1][0] = dp[i][0] + score[c2[i]][' '];
}

int main()
{
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    while(n--)
    {
        cin >> len1 >> c1;
        cin >> len2 >> c2;
        init();
        for(int i = 1; i <= len1; i++)
            for(int j = 1; j <= len2; j++)
                dp[j][i] = max(max(dp[j - 1][i - 1] + score[c2[j - 1]][c1[i - 1]], dp[j - 1][i] + score[c2[j - 1]][' ']),
                               dp[j][i - 1] + score[c1[i - 1]][' ']);
        cout << dp[len2][len1] << endl;
    }
    return 0;
}

最长公共子串（连续）

和LCS区别是区别就是因为是连续的，如果两个元素不等，那么就要=0了而不能用之前一个状态的最大元素

区间DP

区间dp，顾名思义就是在一段区间上进行动态规划。对于每段区间，他们的最优值都是由几段更小区间的最优值得到，是分治思想的一种应用，将一个区间问题不断划分为更小的区间直至一个元素组成的区间，枚举他们的组合 ，求合并后的最优值。

算法结构

1

设F[i,j]（1<=i<=j<=n）表示区间[i,j]内的数字相加的最小代价
每次用变量k（i<=k<=j-1）将区间分为[i,k]和[k+1,j]两段

For l:=2 to n do // 枚举区间长度
for i:=1 to n do // 枚举区间的左端点
begin
j:=i+l-1; // 计算区间的右端点,因为区间长度和左端点循环嵌套枚举，保证了[i,j]内的所有子区间都被枚举到
if j>n then break; // 保证了下标不越界
for k:= i to j-1 do // 状态转移，去推出 f[i,j]
f[i , j]= max{f[ i,k]+ f[k+1,j]+ w[i,j] }
end;

作者：Steven1997
链接：https://www.jianshu.com/p/9c6401ea2f9b
來源：简书
简书著作权归作者所有，任何形式的转载都请联系作者获得授权并注明出处。

1
2
3
4
5
6
7

## [poj 1651 Multiplication Puzzle (区间dp)](http://poj.org/problem?id=1651)

**题意**

​```c++
给出一个数组a，可以将其中除了头尾两个数之外的任何一个数字a[i]取出数列，需要的花费为   a[i-1] * a[i] * a[i+1]，问如果需要把这个数列除了头尾之外的数字都取完，怎样的取出顺序是花费最小的，输出这个最小花费

如果贪心每次取最小的话是错的，看下面一组测试

1
2
5
1 2 1 100 1

思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
首先我们可以考虑最小的一个可以操作的区间为3个数字，是可以直接算出答案的。
对于长度小于3的区间，我们可以直接得到 dp[i][i] = 0;

对于长度大于3的区间，我们可以在其中找到一个中点，例如区间 i ~ j  取中点k 即分为区间  i~k 和 k+1~j, 对于区间 i~k 我们有答案 dp[i][k]  对于区间 k+1~j 我们有答案  dp[k+1][j] ，而在这两个区间运算完之后 会剩下的是 a[i],a[k+1],a[j+1]，所以为了消除k我们会有花费 a[i] * a[k+1] * a[j+1]，即转移方程 ：

dp[i][j]= min(dp[i][k] + dp[k + 1][j] + arr[i] * arr[k + 1] * arr[j + 1]);


先计算ans[i][i + 1] ( 1 <= i < N – 1 )，ans[i][i + 2] ( 1 <= i < N – 2 )，……
即计算ans[i][i + j] ( 1 <= j < N – 1, 1 <= i < N – j )

那么可以这样写
for(int j = 1; j <= n - 1; j++) //看上面j的取值范围
        for(int i = 1; i <= n - j; i++) //看上面i的取值范围
        {
            dp[i][i + j] = INF; //取的是最小，可以初始化为无穷大
            for(int k = i; k < i + j; k++) //从给出的区间[i, i + j]的左边开始,一直到右边
            {
                dp[i][i + j]= min(dp[i][k] + dp[k + 1][i + j] + arr[i] * arr[k + 1] * arr[i + j + 1], dp[i][i + j]);
            }
        }

参考：

http://www.voidcn.com/article/p-xcolbvjf-bke.html

https://111qqz.com/2016/07/poj-1651/

http://www.acmsearch.com/article/show/16953

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-08-11 12:08:14
 Exe.Time:0MS	 Exe.Memory：624k
*/
#include <iostream>
#include <algorithm>
using namespace std;

const int INF = 1e10;
const int MAXN = 1E3;
int dp[MAXN][MAXN];
int arr[MAXN];

int main()
{
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> arr[i];
        dp[i][i] = 0;
    }

    for(int j = 1; j <= n - 1; j++)
        for(int i = 1; i <= n - j; i++)
        {
            dp[i][i + j] = INF;
            for(int k = i; k < i + j; k++)
            {
                dp[i][i + j]= min(dp[i][k] + dp[k + 1][i + j] + arr[i] * arr[k + 1] * arr[i + j + 1], dp[i][i + j]);
            }
        }
    cout<<dp[1][n - 1]<<endl;
    return 0;
}

LeetCode664 Strange Printer 奇怪的打印机

题解：

http://www.cnblogs.com/grandyang/p/8319913.html

刷题找工作—-leetcode 664 —bili

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int strangePrinter(string s) 
    {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        for (int i = n - 1; i >= 0; --i) 
        {
            for (int j = i; j < n; ++j) 
            {
                dp[i][j] = (i == j) ? 1 : (1 + dp[i + 1][j]); //取的min，可以先考虑最坏情况
                for (int k = i + 1; k <= j; ++k) 
                {
                    if (s[k] == s[i]) dp[i][j] = min(dp[i][j], dp[i + 1][k - 1] + dp[k][j]);
                }
            }
        }
        return (n == 0) ? 0 : dp[0][n - 1];
    }
};

Leetcode 813. Largest Sum of Averages

题解：

https://blog.csdn.net/magicbean2/article/details/79893634

刷题找工作—-leetcode 813 —bili

递推版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/*
Status: Accepted
Runtime: 4 ms
Submitted: 下午5:16,星期日, 2018年8月12日
*/
class Solution 
{
public:
    double largestSumOfAverages(vector<int>& A, int K) 
    {
        const int n = A.size();
        m_ = vector<vector<double>>(K + 1, vector<double>(n + 1, 0.0)); //下标从1开始，初始化为0，代表没有求解过
        sums_ = vector<double>(n + 1, 0.0); //前i个元素的和
        for(int i = 1; i <= n; i++)
            sums_[i] = sums_[i - 1] + A[i - 1]; //suns_[i]存的是前i个元素和
        return LSA(A, n, K); //在A中有n个元素分为k组
    }
private:
    vector<vector<double>> m_;
    vector<double> sums_;
    
    double LSA(const vector<int>& A, int n, int k)
    {
        if(m_[k][n] > 0) //记忆化，求解过的话就直接返回
            return m_[k][n];
        if(k == 1) 
            return sums_[n] / n; //递归结束
        //i是分割点，将前n个元素分为两半，一个是1～i，另一个是i+1～n
        //递归求解i个元素分成k-1组能取的最大值
        //因为是k-1组，所以得至少有k-1个元素，i从k - 1开始
        for(int i = k - 1; i < n; i++)
         	m_[k][n] = max(m_[k][n], LSA(A, i, k - 1) + (sums_[n] - sums_[i]) / (n - i));
        //sum_[n] - sums_[i]：i+1～n的和
        return m_[k][n];                   
    }
};

DP版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
51 / 51 test cases passed.
Status: Accepted
Runtime: 12 ms
Submitted: 下午5:21,星期日, 2018年8月12日
*/
class Solution 
{
public:
    double largestSumOfAverages(vector<int>& A, int K)
    {
         const int n = A.size();
       	 //下标从1开始，初始化为0，代表没有求解过
       	 vector<vector<double>> dp(K + 1, vector<double>(n + 1, 0.0));
         //前i个元素的和
         vector<double>sums(n + 1, 0.0);
         for(int i = 1; i <= n; i++)
         {
             sums[i] = sums[i - 1] + A[i - 1]; //suns_[i]存的是前i个元素和
             dp[1][i] = sums[i] / i; //前i个元素化分为一组的平均数
         }
          
         for(int k = 2; k <= K; k++) //第一组已经分了，组的个数从2开始
             for(int i = k; i <= n; i++) //使用i个元素，化分为k组，至少k个元素
                 //j是分割点，把前i个元素分为两半,一半是1~j,另一半是j+1~i
                 for(int j = k - 1; j < i; j++) 
                 {
                     //把i个元素分成k组取得的最大值
                     dp[k][i] = max(dp[k][i], dp[k - 1][j] + (sums[i] - sums[j]) / (i - j));
                 }
          return dp[K][n];             
    }
};

因为dp[k]只与dp[k - 1]有关。所以可以降维

降维版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/*
51 / 51 test cases passed.
Status: Accepted
Runtime: 4 ms
Submitted: Submitted: 下午5:23,星期日, 2018年8月12日
*/
class Solution 
{
public:
    double largestSumOfAverages(vector<int>& A, int K)
    {
         const int n = A.size();
       	 vector<double> dp(n + 1, 0.0); //改
         vector<double> sums(n + 1, 0.0);
         for(int i = 1; i <= n; i++)
         {
             sums[i] = sums[i - 1] + A[i - 1];
             dp[i] = sums[i] / i; //改 
         }
          
         for(int k = 2; k <= K; k++) 
         {
             vector<double> tmp(n + 1, 0.0); //tmp存的是当前k的最大值，dp存的是k-1
             for(int i = k; i <= n; i++) 
                 for(int j = k - 1; j < i; j++) 
                 {
                   //  dp[k][i] = max(dp[k][i], dp[k - 1][j] + (sums[i] - sums[j]) / (i - j));
                     tmp[i] = max(tmp[i], dp[j] + (sums[i] - sums[j]) / (i - j));
                 }
             dp.swap(tmp);
         }
         return dp[n];             
    }
};

POJ 1160区间DP+平行四边形优化(Post Office)

题意

有n个村庄现在要建立m个邮局，问怎么建邮局才能使得村庄到最近的邮局距离和最小。输出距离和即可。

思路

1
一般的区间dp是从小区间到大区间，而此题在此之外还有一个限制是m个邮局。对于此类问题可以直接建立dp的时候加上限制条件：dp[i][j]=min(dp[k][j−1]+one[k+1][i]) 定义dp含义为前i个村庄建立了j个邮局的最小距离和，那么在建立第j的时候可以枚举之前已经求出的区间，从j-1个邮局的前提下加上现在的1个邮局，one[i][j] 的含义是在区间i到j 的范围之中建立一个邮局，其实也就是中位数的位置，然后递推找出最小的值即可。

参考：

https://blog.csdn.net/since_natural_ran/article/details/77629901

未用优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-07-27 20:33:12		
 Exe.Time:94MS	 Exe.Memory：5.3MB
*/

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int len = 1e3;

int dp[len][len]; //前i个村庄建立了j个邮局的最小距离和
int onePost[len][len] = {0}; //i到j 的范围之中建立一个邮局最小距离
int arr[len];
int numV, numP;

void init()
{
    for(int i = 1; i <= numV; i++)
        for(int j = i; j <= numV; j++)
            onePost[i][j] = onePost[i][j - 1] + arr[j] - arr[(i + j) / 2]; //中位数位置，加多一个数，同时取其中位数，则需要添加的距离为 arr[j] - arr[(i + j) / 2]
    
    memset(dp, 0x3f, sizeof(dp)); //因为是取min，所以可以初始化dp数组为较大值
    for(int i = 0; i <= numP; ++i)
        dp[i][i] = 0; //前i个村庄建立了i个邮局，则距离为0
}

int main()
{
    ios::sync_with_stdio(false);
    cin >> numV >> numP;
    for(int i = 1; i <= numV; i++)
        cin >> arr[i];
    init();

    for(int i = 1; i <= numV; i++) //村庄数量，[1,numV]
        for(int j = 1; j <= numP; j++) //邮局数量，小于等于numP
            for(int k = j - 1; k < i; k++)
                dp[i][j] = min(dp[i][j], dp[k][j - 1] + onePost[k + 1][i]);
    cout << dp[numV][numP];
    return 0;
}

优化

参考：

https://blog.csdn.net/since_natural_ran/article/details/77629901

https://blog.csdn.net/u012139398/article/details/43956985

http://www.cnblogs.com/vongang/archive/2013/01/21/2869315.html

四边形优化公式:

1
ss[i, j-1] <= ss[i,j] <= ss[i + 1, j]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int numVillages, numPost;
const int MAXN = 1E3;
int dp[MAXN][MAXN];
int onePost[MAXN][MAXN];
int arr[MAXN];
int ss[MAXN][MAXN]; //ss[i][j]表示dp[i][j]取得最优解时，最后一个邮局设立在城市的编号,即决策变量

void init()
{
    memset(dp, 0x3f, sizeof(dp));
    memset(ss, 0, sizeof(ss));
    for(int i = 0; i<= numPost; i++)
        dp[i][i] = 0;

    for(int i = 1; i <= numVillages; i++)
        for(int j = i; j <= numVillages; j++)
            onePost[i][j] = onePost[i][j - 1] + arr[j] - arr[(i + j) / 2];
}

int main()
{
    ios::sync_with_stdio(false);
    cin >> numVillages >> numPost;
    for(int i = 1; i <= numVillages; i++)
        cin >> arr[i];
    init();
    for(int i = 1; i <= numVillages; i++)
    {
        for(int j = 1; j <= numPost; j++)
        {
            ss[i + 1][j] = i + 1; //不知道i，j关系，默认搜索完所有的村庄
            for(int k = ss[i][j - 1]; k <= ss[i + 1][j]; k++)
            {
                if(dp[i][j] > dp[k][j - 1] + onePost[k + 1][i])
                {
                    dp[i][j] = dp[k][j - 1] + onePost[k + 1][i];
                    ss[i][j] = k;
                }
            }
        }
    }

    cout << dp[numVillages][numPost] << endl;
    return 0;
}

压缩二维最大子序列和

HDU1081(To The Max)

题意:大致是求二维数组的最大矩阵和。

参考：

https://www.cnblogs.com/BlackStorm/p/4922207.html

https://blog.csdn.net/linraise/article/details/16349527

https://blog.csdn.net/hitwhylz/article/details/11848439

二维压缩成一维，然后按照求最大序列和的办法去求最大值就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-09-04 19:59:05			
 Exe.Time:15MS	 Exe.Memory：1892k
*/
#include <iostream>
#include <climits>
#include <cstring>
#include <algorithm>
using namespace std;

const int MAXN = 200;
int arr[MAXN][MAXN];
int cntRow[MAXN];
int n;

int maxSubArr() //求一维最大序列和
{
    int dp[MAXN] = {0};
    int MAX = INT_MIN;
    for(int i = 1; i <= n; ++i)
    {
        dp[i] = max(dp[i - 1] + cntRow[i], cntRow[i]); //最大子序列和转移方程
        if(MAX < dp[i])
            MAX = dp[i];
    }
    return MAX;
}

int solve()
{
    int ans = INT_MIN;
    for(int i = 1; i <= n; ++i)　//压缩
    {
        memset(cntRow, 0, sizeof(cntRow));
        for(int j = i; j <= n; ++j)　
        {
            for(int k = 0; k <= n; ++k)
                cntRow[k] += arr[j][k];
            int tmp = maxSubArr();
            if (tmp > ans)
                ans = tmp;
        }
    }
    return ans;
}

int main()
{
    while(cin >> n)
    {
        for(int i = 1; i <= n; ++i)
        {
            for(int j = 1; j <= n; ++j)
            {
                cin >> arr[i][j];
            }
        }
        cout << solve() << endl;
    }
    return 0;
}

杂项二维dp转移

POJ2192 (Zipper)－－－判断两个字符串能否合成一个字符串

题意：给你三个字符串，问你能否由前两个合成第三个，且要求不改变前两个字符串的顺序。题目保证第三个字符串的长度为前两个字符串的长度之和。

参考：

https://www.cnblogs.com/huashanqingzhu/p/7348218.html

1
2
3
4
5
最优子结构分析：如果A、B可以组成C，那么，C最后一个字母，必定是 A 或 B 的最后一个字母组成。
C去除除最后一位，就变成是否可以求出 A-1和B 或者 A与B-1 与 是否可以构成 C-1。。。
 状态转移方程：
用f[i][j] 表示 A前 i 位 和B 前j 位是否可以组成 C的前i+j位
             dp[i][j]= (dp[i-1][j]&&(a[i]==c[i+j]))||(dp[i][j-1]&&(b[j]==c[i+j]))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-07-30 16:52:10		
 Exe.Time:407MS	 Exe.Memory：4048KB
*/

#include <iostream>
#include <cstring>
using namespace std;

const int MAXN = 1E3;
char a[MAXN], b[MAXN], c[MAXN];
int dp[MAXN][MAXN];

int main()
{
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    for(int k = 1; k <= n; k++)
    {
        memset(dp, 0, sizeof(dp));
        a[0] = b[0] = c[0] = ' ';
        cin >> a + 1>> b + 1>> c + 1;
        int lenA = strlen(a);
        int lenB = strlen(b);
        int lenC = strlen(c);

        for(int i = 0; i < lenA; i++) //初始化，单独ａ与ｃ匹配
        {
            if(a[i] == c[i])　
                dp[i][0] = 1;
        }

        for(int i = 0; i < lenB; i++) //初始化，单独ｂ与ｃ匹配
        {
            if(b[i] == c[i])
                dp[0][i] = 1;
        }

        for(int i = 1; i <= lenA; i++)
            for(int j = 1; j <= lenB; j++)
            {
                dp[i][j] = ( (dp[i - 1][j] && a[i] == c[i + j]) || (dp[i][j - 1] && b[j] == c[i + j]) );
            }

        cout << "Data set " << k << ": ";
        if(dp[lenA][lenB])
             cout << "yes" << endl;
        else
             cout << "no" << endl;
    }
    return 0;
}

POJ3356(AGTC)－－－s2变成s1最少的操作

题意：给出两个字符串x 与 y，其中x的长度为n，y的长度为m，并且m>=n.然后y可以经过删除一个字母，添加一个字母，转换一个字母，三种操作得到x.问最少可以经过多少次操作

参考：

https://blog.csdn.net/u013480600/article/details/40780781

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/*
 Judge Status : Accepted	 Language : C++
 Submit Time：2018-07-30 20:55:35		
 Exe.Time:32MS	 Exe.Memory：4188MB
*/
#include <iostream>
#include <algorithm>
using namespace std;
const int LEN = 1e3 + 10;

int dp[LEN][LEN];
char s1[LEN], s2[LEN];
int n1, n2;

int main()
{
    ios::sync_with_stdio(false);
    while(cin >> n1 >> s1)
    {
        cin >> n2 >> s2;
        //初始化
        for(int i = 0; i <= n1; i++) //s2为空，s1删除字符串变成s2
            dp[i][0] = i;
        for(int i = 0; i <= n2; i++) //s1为空，s1添加字符串变成s2
            dp[0][i] = i;
        for(int i = 1; i <= n1; i++)
            for(int j = 1; j <= n2; j++)
                dp[i][j]=min(dp[i-1][j-1]+(s1[i-1]==s2[j-1]?0:1),
                              min(dp[i-1][j]+1,dp[i][j-1]+1));
        cout << dp[n1][n2] << endl;
    }
    return 0;
}