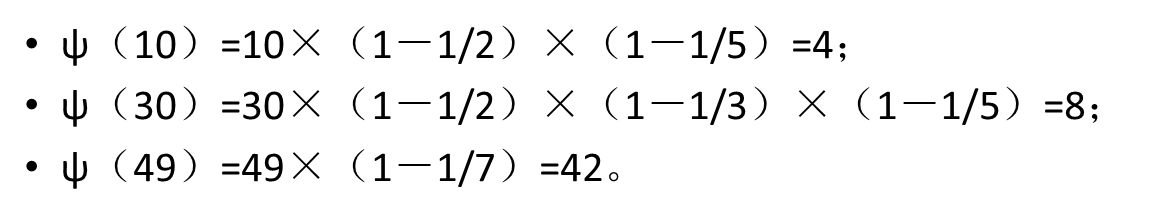欧几里得及其扩展，素数，模运算，快速幂，欧拉函数，快速乘。

欧几里得—最大公约数

gcd（a, b) = gcd(b, a mod b)

1
2
3
4
5
6
int gcd(int a, int b)
{
    if(b == 0)
        return a;
    return gcd(b, a % )b;
}

一波应用：线段上格点个数—-挑战编程—-欧几里得

algorithm库的std::_gcd函数

1
2
3
4
5
6
7
8
9
10
11
12
#include <iostream>
#include <algorithm>
using namespace std;

int main()
{
    int a = 8;
    int b = 12;
    cout <<__gcd(a, b); //两个'_'
    return 0;
}
//out：4   //g++-4.8

最小公倍数(LCM)和最大公约数(GCD)

lcm(a, b) = (a*b)/gcd(a,b)

扩展欧几里得

基本算法：对于不完全为 0 的非负整数 a，b，gcd（a，b）表示 a，b 的最大公约数，必然存在整数对 x，y ，使得 gcd（a，b）=ax+by。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int r=exgcd(b,a%b,x,y);
    int t=x;
    x=y;
    y=t-a/b*y;
    return r;
}

素数

埃氏筛法—-求解n以内的素数个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int prime[MAXN]; //第i个素数的值
bool is_prime[MAXN]; //is_prime[i]为true时表示i是素数

//返回n以内素数的个数
int solve(int n)
{
    int p = 0; //代表素数个数
    for(int i = 2; i <= n; i++)
        is_prime[i] = true;
    for(int i = 2; i <= n; i++)
    {
        if(is_prime[i])
        {
            prime[p++] = i; //每有一个素数，p就++，然后prime存的就是素数的值，然后进行筛选
            for(int j = 2 * i; j <= n; j += i)
                is_prime[j] = false;
        }
    }
    return p; //prime[p - 1]代表n以内最大的素数
}

模运算

一些基本规则

https://blog.csdn.net/x_i_y_u_e/article/details/50823235

除法取模与费马小定理

http://www.cnblogs.com/ECJTUACM-873284962/p/6847672.html

https://blog.csdn.net/liangzhaoyang1/article/details/56514028

快速幂，快速乘

参考：https://blog.xehoth.cc/DurationPlan-modPow/#%E5%8D%81%E8%BF%9B%E5%88%B6%E5%BF%AB%E9%80%9F%E5%B9%82

快速乘

普通快速幂在面对大量数据或单个够大数据时效率很低，这个时候我们就需要十进制快速幂，而如果模数是 long long 以内的数，我们可以用快速幂思想 O(log n)O(log n) 完成快速乘，但我们其实可以 O(1)完成。

利用 long double，而 long double的精度其实只有 19 位，直接乘是不行的，我们可以先除再乘，这样就不会出现精度问题，而前面直接计算 a×b，再减去后面的部分，即使前面 a×b 爆负，它还会再爆一遍变为正的，保证了答案的正确。

1
2
3
4
5
6
typedef long double ld;
typedef long long ll
inline ll mul(ll a, ll b) 
{
    return (a * b - (ll)((ld)a / MOD * b) * MOD + MOD) % MOD;
}

二进制快速幂

基本代码，都懂

1
2
3
4
5
6
7
8
9
10
11
12
13
typedef long long ll;
ll mod_pow(ll x, ll n, ll mod) //x^n % mod
{
    ll ans = 1;
    while(n > 0) //遍历所有二进制位
    {
        if(n & 1) //对应n的二进制位是不是1
            ans = ans * x % mod; //乘上x^(2^i)
        x = x * x % mod;  //x平方
        n >>= 1;
    }
    return ans;
}

蜜汁优化版本（参考ext/numeric.h的power函数）

1
2
3
4
5
6
7
8
9
inline long optimizedModPow(long a, long b) {
    if (b == 0) return 1;
    for (; ~b & 1; b >>= 1, a = mul(a, a));
    register long ret = a;
    for (b >>= 1; b; b >>= 1)
        a = mul(a, a), (b & 1) ? ret = mul(a, ret) : 0;
    return ret;
}
//balabala--看不懂系列！！

十进制快速幂

说白了就是拆成十进制数

欧拉函数

对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目。例如φ(8)=4，因为1,3,5,7均和8互质。

欧拉函数公式

(其中p1, p2……pn为x的所有质因数，x是不为0的整数)

注意：

φ(1) = 1（唯一和1互质的数(小于等于1)就是1本身）。 (注意：每种质因数只一个。比如 那么

性质

  1. 当n为质数时，$φ(n)=n-1$。
  2. 当$n=p^k$时（p是素数），$φ(n)=φ(p^k )=p^k-p^{k-1}=(p-1)p^{k-1}$
  3. 若n,m互质，$φ(nm)=φ(n)φ(m)=(n-1)(m-1)$
  4. 若n是奇数，则$φ(2n)=φ(n)$

特殊性质

  1. 当a与n互质时(n>2)有:$a^{φ(n)}\ mod\ n=1$ (恒等于)此公式即 欧拉定理
  2. 当a与n互质且n为质数时(即:gcd(a,n)=1)则上式有:$ a^{(n-1)}\ mod \ n=1$(恒等于)此公式即 费马小定理

延伸

小于n且与n互质的数的和：

应用

求$7^{222}$的个位数。

因为7和10互质，且$φ(10)=4$

所以$7^4 mod 10=1$

所以$7^{222} mod 10=7^{4∗55}∗7^2 mod 10=7^2 mod 10=9$

即$7^{222} mod 10=7^{222\%4} mod 10=7^2 mod 10=9$

模板

参考：

https://www.cnblogs.com/wkfvawl/p/9317125.html

直接求小于或等于n,且与n互质的个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int  eular(int n)
{
    int i,ret=n;
    for(i=2; i<=sqrt(n); i++)
    {
        if(n%i==0)
        {
            ret=ret/i*(i-1);//这里先使用除法是为了防止溢出，ret=ret*(1-1/p(1))
            //为了完全消除我们已经除完了刚才得到的那个i因子,确保下一个得到的i是n的素因子
            while(n%i==0)
            {
                n/=i;
            }
        }
    }
    if(n>1)//可能还剩下一个素因子没有除 
    {
        ret=ret/n*(n-1);
    }
    return ret;
}
筛选模板:求[1,n]之间每个数的质因数的个数

如果我们要求的数比较多，如果一个一个求那么很容易就超时，所以我们自然而然就想到——打表。

如果我们依照上述思想，来个最朴素的打表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#define size 1000001
int euler[size];
void Init()
{
    euler[1]=1;
    for(int i=2; i<size; i++)
    {
        if(!euler[i])
        {
            for(int j=i; j<size; j+=i)
            {
                if(!euler[j])
                {
                    euler[j]=j;
                }
                euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出
            }
        }
    }
}